
【題目】將函數f(x)=2sin(2x﹣![]() )的圖象向左平移
)的圖象向左平移![]() 個單位,再向上平移1個單位,得到函數y=g(x)的圖象,若y=g(x)在[0,b](b>0)上至少含有10個零點,則b的最小值為
個單位,再向上平移1個單位,得到函數y=g(x)的圖象,若y=g(x)在[0,b](b>0)上至少含有10個零點,則b的最小值為
【答案】![]()
【解析】將函數f(x)=2sin(2x﹣![]() )的圖象向左平移
)的圖象向左平移![]() 個單位,可得y=2sin[2(x+
個單位,可得y=2sin[2(x+![]() )﹣
)﹣![]() ]=2sin2x的圖象;
]=2sin2x的圖象;
再向上平移1個單位,得到函數y=g(x)=2sin2x+1的圖象,
再由y=g(x)在[0,b](b>0)上至少含有10個零點,可得方程sin2x=﹣![]() 至少有10個解,
至少有10個解,
則b的最小值4×π+![]() =
=![]() ,
,
所以答案是:![]() .
.
【考點精析】本題主要考查了函數y=Asin(ωx+φ)的圖象變換的相關知識點,需要掌握圖象上所有點向左(右)平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數
倍(橫坐標不變),得到函數![]() 的圖象才能正確解答此題.
的圖象才能正確解答此題.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的兩個焦點分別為
的兩個焦點分別為![]() 和
和![]() ,短軸的兩個端點分別為
,短軸的兩個端點分別為![]() 和
和![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,且滿足
上,且滿足![]() ,當
,當![]() 變化時,給出下列三個命題:
變化時,給出下列三個命題:
①點![]() 的軌跡關于
的軌跡關于![]() 軸對稱;②
軸對稱;②![]() 的最小值為2;
的最小值為2;
③存在![]() 使得橢圓
使得橢圓![]() 上滿足條件的點
上滿足條件的點![]() 僅有兩個,
僅有兩個,
其中,所有正確命題的序號是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,“cosA>cosB”是“sinA<sinB”的 ( )
A.充分非必要條件
B.必要非充分條件
C.充要條件
D.既非充分又非必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩名同學參加2018年高考,根據高三年級一年來的各種大、中、小型數學模擬考試總結出來的數據顯示,甲、乙兩人能考140分以上的概率分別為![]() 和
和![]() ,甲、乙兩人是否考140分以上相互獨立,則預估這兩個人在2018年高考中恰有一人數學考140 分以上的概率為( )
,甲、乙兩人是否考140分以上相互獨立,則預估這兩個人在2018年高考中恰有一人數學考140 分以上的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某射擊游戲規定:每位選手最多射擊3次;射擊過程中若擊中目標,方可進行下一次射擊,否則停止射擊;同時規定第i(i=1,2,3)次射擊時擊中目標得4﹣i分,否則該次射擊得0分.已知選手甲每次射擊擊中目標的概率為0.8,且其各次射擊結果互不影響.
(Ⅰ)求甲恰好射擊兩次的概率;
(Ⅱ)設該選手甲停止射擊時的得分總和為ξ,求隨機變量ξ的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin(ωx),其中常數ω>0
(1)令ω=1,判斷函數![]() 的奇偶性,并說明理由;
的奇偶性,并說明理由;
(2)令ω=2,將函數y=f(x)的圖象向左平移個![]() 單位,再向上平移1個單位,得到函數y=g(x)的圖象,對任意a∈R,求y=g(x)在區間[a,a+10π]上零點個數的所有可能值.
單位,再向上平移1個單位,得到函數y=g(x)的圖象,對任意a∈R,求y=g(x)在區間[a,a+10π]上零點個數的所有可能值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知圓![]() 與
與![]() 軸交于
軸交于![]() 兩點(
兩點(![]() 在
在![]() 的上方),直線
的上方),直線![]() .
.

(1)當![]() 時,求直線
時,求直線![]() 被圓
被圓![]() 截得的弦長;
截得的弦長;
(2)若![]() ,點
,點![]() 為直線
為直線![]() 上一動點(不在
上一動點(不在![]() 軸上),直線
軸上),直線![]() 的斜率分別為
的斜率分別為![]() ,直線
,直線![]() 與圓的另一交點分別
與圓的另一交點分別![]() .
.
①問是否存在實數![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,說明理由;
的值;若不存在,說明理由;
②證明:直線![]() 經過定點,并求出定點坐標.
經過定點,并求出定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:
(單位:![]() )和年利潤
)和年利潤![]() (單位:千元)的影響,對近8年的年宣傳費
(單位:千元)的影響,對近8年的年宣傳費![]() 和年銷售量
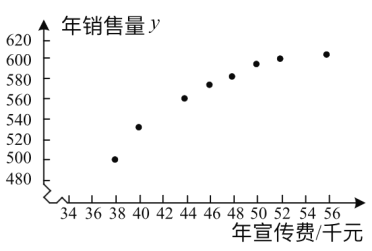
和年銷售量![]() 數據作了初步處理,得到下面的散點圖及一些統計量的值.
數據作了初步處理,得到下面的散點圖及一些統計量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 298.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
,![]()
(1)根據散點圖判斷,![]() 與
與![]() 哪一個適宜作為年銷售量
哪一個適宜作為年銷售量![]() 關于年宣傳費
關于年宣傳費![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)以知這種產品的年利率![]() 與
與![]() 、
、![]() 的關系為
的關系為![]() .根據(2)的結果求年宣傳費
.根據(2)的結果求年宣傳費![]() 時,年銷售量及年利潤的預報值是多少?
時,年銷售量及年利潤的預報值是多少?
附:對于一組數據![]() ,
,![]() ……
……![]() ,其回歸線
,其回歸線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,側面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中點.
(Ⅰ)求證:DE⊥平面PBC;
(Ⅱ)求二面角A﹣PD﹣E的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com