
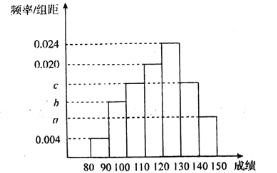
【題目】高三年級某班50名學生期中考試數(shù)學成績的頻率分布直方圖如圖所示,成績分組區(qū)間為:![]()
![]()
![]()
![]()
![]()
![]()
![]() .其中a,b,c成等差數(shù)列且
.其中a,b,c成等差數(shù)列且![]() .物理成績統(tǒng)計如表.(說明:數(shù)學滿分150分,物理滿分100分)
.物理成績統(tǒng)計如表.(說明:數(shù)學滿分150分,物理滿分100分)
分組 |
|
|
|
|
|
頻數(shù) | 6 | 9 | 20 | 10 | 5 |
(1)根據(jù)頻率分布直方圖,請估計數(shù)學成績的平均分;
(2)根據(jù)物理成績統(tǒng)計表,請估計物理成績的中位數(shù);
(3)若數(shù)學成績不低于140分的為“優(yōu)”,物理成績不低于90分的為“優(yōu)”,已知本班中至少有一個“優(yōu)”同學總數(shù)為6人,從此6人中隨機抽取3人,記X為抽到兩個“優(yōu)”的學生人數(shù),求X的分布列和期望值.
【答案】(1)![]() (分);(2)75分;(3)見解析.
(分);(2)75分;(3)見解析.
【解析】
(1)根據(jù)頻率之和等于![]() ,a,b,c成等差數(shù)列,
,a,b,c成等差數(shù)列,![]() ,解出
,解出![]() 的值,利用頻率分布直方圖,求出平均分;(2)根據(jù)物理成績統(tǒng)計表,得到中位數(shù)所在的成績區(qū)間,得到答案;(3)根據(jù)數(shù)學成績“優(yōu)”和物理成績“優(yōu)”,得到兩科均為“優(yōu)”的人數(shù),計算出每種情況的概率,寫出分布列,得到期望值.
的值,利用頻率分布直方圖,求出平均分;(2)根據(jù)物理成績統(tǒng)計表,得到中位數(shù)所在的成績區(qū)間,得到答案;(3)根據(jù)數(shù)學成績“優(yōu)”和物理成績“優(yōu)”,得到兩科均為“優(yōu)”的人數(shù),計算出每種情況的概率,寫出分布列,得到期望值.
(1)根據(jù)頻率分布直方圖得,![]()
又因![]()
![]() ,
,
解得![]()
![]()
![]() ,
,
故數(shù)學成績的平均分
![]()
![]() (分),
(分),
(2)總?cè)藬?shù)50分,由物理成績統(tǒng)計表知,中位數(shù)在成績區(qū)間![]() ,
,
所以物理成績的中位數(shù)為75分.
(3)數(shù)學成績?yōu)椤皟?yōu)”的同學有4人,物理成績?yōu)椤皟?yōu)”有5人,
因為至少有一個“優(yōu)”的同學總數(shù)為6名同學,
故兩科均為“優(yōu)”的人數(shù)為3人,
故X的取值為0、1、2、3.
![]()
![]()
![]()
![]() .
.
所以分布列為:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
期望值為:
![]()
![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中點(如圖1),將
是EA的中點(如圖1),將![]() 沿CD折起到圖2中
沿CD折起到圖2中![]() 的位置,得到四棱錐是
的位置,得到四棱錐是![]() .
.
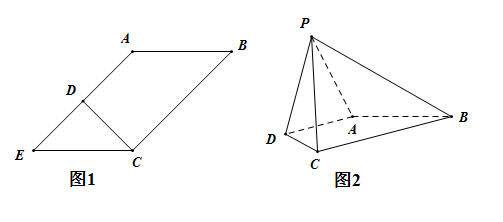
(1)求證:![]() 平面PDA;
平面PDA;
(2)若PD與平面ABCD所成的角為![]() .且
.且![]() 為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 在
在![]() 上的單調(diào)區(qū)間;
上的單調(diào)區(qū)間;
(2)用![]() 表示
表示![]() 中的最大值,
中的最大值,![]() 為
為![]() 的導函數(shù),設(shè)函數(shù)
的導函數(shù),設(shè)函數(shù)![]() ,若
,若![]() 在
在![]() 上恒成立,求實數(shù)
上恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)O為坐標原點,動點M在橢圓C![]() 上,過M作x軸的垂線,垂足為N,點P滿足
上,過M作x軸的垂線,垂足為N,點P滿足![]() .
.
(1)求點P的軌跡方程;
(2)設(shè)點![]() 在直線
在直線![]() 上,且
上,且![]() .證明:過點P且垂直于OQ的直線
.證明:過點P且垂直于OQ的直線![]() 過C的左焦點F.
過C的左焦點F.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了調(diào)節(jié)高三學生學習壓力,某校高三年級舉行了拔河比賽,在賽前三位老師對前三名進行了預測,于是有了以下對話:老師甲:“7班男生比較壯,7班肯定得第一名”.老師乙:“我覺得14班比15班強,14班名次會比15班靠前”.老師丙:“我覺得7班能贏15班”.最后老師丁去觀看完了比賽,回來后說:“確實是這三個班得了前三名,且無并列,但是你們?nèi)酥兄挥幸蝗祟A測準確”.那么,獲得一、二、三名的班級依次為( )
A.7班、14班、15班B.14班、7班、15班
C.14班、15班、7班D.15班、14班、7班
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)).以坐標原點為極點,
為參數(shù)).以坐標原點為極點,![]() 軸的非負半軸為極軸且取相同的單位長度建立極坐標系,圓
軸的非負半軸為極軸且取相同的單位長度建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與圓
的普通方程與圓![]() 的直角坐標方程;
的直角坐標方程;
(2)設(shè)動點![]() 在圓
在圓![]() 上,動線段
上,動線段![]() 的中點
的中點![]() 的軌跡為
的軌跡為![]() ,
,![]() 與直線
與直線![]() 交點為
交點為![]() ,且直角坐標系中,
,且直角坐標系中,![]() 點的橫坐標大于
點的橫坐標大于![]() 點的橫坐標,求點
點的橫坐標,求點![]() 的直角坐標.
的直角坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】三棱柱ABC﹣A1B1C1中,平面AA1B1B⊥平面ABC,AB=AA1=A1B=4,BC=2,AC=2![]() ,點F為AB的中點,點E為線段A1C1上的動點.
,點F為AB的中點,點E為線段A1C1上的動點.
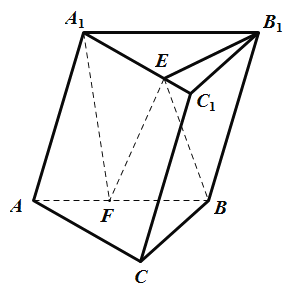
(1)求證:BC⊥平面A1EF;
(2)若∠B1EC1=60°,求四面體A1B1EF的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() :
:![]() ,動直線l與橢圓E交于不同的兩點
,動直線l與橢圓E交于不同的兩點![]() ,
,![]() ,且△AOB的面積為1,其中O為坐標原點.
,且△AOB的面積為1,其中O為坐標原點.
(1)證明:![]() 為定值;
為定值;
(2)設(shè)線段AB的中點為M,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,左、右焦點分別是
,左、右焦點分別是![]() ,橢圓
,橢圓![]() 上短軸的一個端點與兩個焦點構(gòu)成的三角形的面積為
上短軸的一個端點與兩個焦點構(gòu)成的三角形的面積為![]() ;
;
(1)求橢圓![]() 的方程;
的方程;
(2)過![]() 作垂直于
作垂直于![]() 軸的直線
軸的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點(點
兩點(點![]() 在第二象限),
在第二象限),![]() 是橢圓上位于直線
是橢圓上位于直線![]() 兩側(cè)的動點,若
兩側(cè)的動點,若![]() ,求證:直線
,求證:直線![]() 的斜率為定值.
的斜率為定值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com