
【題目】已知△ABC的內(nèi)角A,B,C所對(duì)的邊分別為a,b,c,且A=2C.
(1)若△ABC為銳角三角形,求 ![]() 的取值范圍;
的取值范圍;
(2)若b=1,c=3,求△ABC的面積.
【答案】
(1)解:由題意:A=2C.
由正弦定理可得, ![]() ,
,
∵△ABC為銳角三角形,
∴ 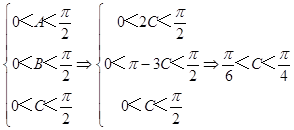 ,
,
進(jìn)而可知, ![]() ,
,
即 ![]() 的取值范圍是
的取值范圍是 ![]() ;
;
(2)解:由(1)可知, ![]() ,
,
∴a=2ccosC=6cosC,
由余弦定理可知,c2=a2+b2﹣2abcosC,即9=36cos2C+1﹣12cos2C,
∵A=2C,
∴C為銳角,
解得 ![]() ,
,
∴ ![]() ,
, ![]()
從而△ABC的面積為 ![]() .
.
(由sinB=sin3C=3sinC﹣4sin3C結(jié)合正弦定理求得 ![]() 亦可)
亦可)
【解析】(1)根據(jù)A=2C,由正弦定理化簡(jiǎn),將 ![]() 的比值轉(zhuǎn)化為三角函數(shù)問(wèn)題,利用三角函數(shù)的有界限可得取值范圍.(2)根據(jù)b=1,c=3,A=2C.建立方程求出a和sinC,可得△ABC的面積.
的比值轉(zhuǎn)化為三角函數(shù)問(wèn)題,利用三角函數(shù)的有界限可得取值范圍.(2)根據(jù)b=1,c=3,A=2C.建立方程求出a和sinC,可得△ABC的面積.
【考點(diǎn)精析】解答此題的關(guān)鍵在于理解余弦定理的定義的相關(guān)知識(shí),掌握余弦定理:![]() ;
;![]() ;
;![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】以平面直角坐標(biāo)系的原點(diǎn)為極點(diǎn),以x軸的正半軸為極軸建立極坐標(biāo)系.設(shè)曲線(xiàn)C的參數(shù)方程為 ![]() (α是參數(shù)),直線(xiàn)l的極坐標(biāo)方程為ρcos(θ+
(α是參數(shù)),直線(xiàn)l的極坐標(biāo)方程為ρcos(θ+ ![]() )=2
)=2 ![]() .
.
(1)求直線(xiàn)l的直角坐標(biāo)方程和曲線(xiàn)C的普通方程;
(2)設(shè)點(diǎn)P為曲線(xiàn)C上任意一點(diǎn),求點(diǎn)P到直線(xiàn)l的距離的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
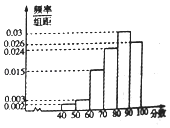
【題目】2017年3月14日,“ofo共享單車(chē)”終于來(lái)到蕪湖,ofo共享單車(chē)又被親切稱(chēng)作“小黃車(chē)”是全球第一個(gè)無(wú)樁共享單車(chē)平臺(tái),開(kāi)創(chuàng)了首個(gè)“單車(chē)共享”模式.相關(guān)部門(mén)準(zhǔn)備對(duì)該項(xiàng)目進(jìn)行考核,考核的硬性指標(biāo)是:市民對(duì)該項(xiàng)目的滿(mǎn)意指數(shù)不低于0.8,否則該項(xiàng)目需進(jìn)行整改,該部門(mén)為了了解市民對(duì)該項(xiàng)目的滿(mǎn)意程度,隨機(jī)訪問(wèn)了使用共享單車(chē)的100名市民,并根據(jù)這100名市民對(duì)該項(xiàng)目滿(mǎn)意程度的評(píng)分,繪制了如下頻率分布直方圖: (I)為了了解部分市民對(duì)“共享單車(chē)”評(píng)分較低的原因,該部門(mén)從評(píng)分低于60分的市民中隨機(jī)抽取2人進(jìn)行座談,求這2人評(píng)分恰好都在[50,60)的概率;
(II)根據(jù)你所學(xué)的統(tǒng)計(jì)知識(shí),判斷該項(xiàng)目能否通過(guò)考核,并說(shuō)明理由.
(注:滿(mǎn)意指數(shù)= ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)= 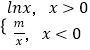 ,若f(x)﹣f(﹣x)=0有四個(gè)不同的根,則m的取值范圍是( )
,若f(x)﹣f(﹣x)=0有四個(gè)不同的根,則m的取值范圍是( )
A.(0,2e)
B.(0,e)
C.(0,1)
D.(0, ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=(x﹣1)lnx﹣(x﹣a)2(a∈R). (Ⅰ)若f(x)在(0,+∞)上單調(diào)遞減,求a的取值范圍;
(Ⅱ)若f(x)有兩個(gè)極值點(diǎn)x1 , x2 , 求證:x1+x2> ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知曲線(xiàn)C1的參數(shù)方程為  (為參數(shù)).在以坐標(biāo)原點(diǎn)為極點(diǎn),軸的正半軸為極軸的極坐標(biāo)系中,曲線(xiàn)C2:
(為參數(shù)).在以坐標(biāo)原點(diǎn)為極點(diǎn),軸的正半軸為極軸的極坐標(biāo)系中,曲線(xiàn)C2: ![]() .
.
(1)求曲線(xiàn)C1的普通方程和C2的直角坐標(biāo)方程;
(2)若C1與C2相交于A、B兩點(diǎn),設(shè)點(diǎn)F(1,0),求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知△ABC的內(nèi)角A,B,C的對(duì)邊分別為a,b,c,且滿(mǎn)足cos2B﹣cos2C﹣sin2A=sinAsinB.
(1)求角C;
(2)若c=2 ![]() ,△ABC的中線(xiàn)CD=2,求△ABC面積S的值.
,△ABC的中線(xiàn)CD=2,求△ABC面積S的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=2sin(ωx+φ)+1(ω>0,|φ|≤ ![]() ),其圖象與直線(xiàn)y=﹣1相鄰兩個(gè)交點(diǎn)的距離為π,若f(x)>1對(duì)x∈(﹣
),其圖象與直線(xiàn)y=﹣1相鄰兩個(gè)交點(diǎn)的距離為π,若f(x)>1對(duì)x∈(﹣ ![]() ,
, ![]() )恒成立,則φ的取值范圍是( )
)恒成立,則φ的取值范圍是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在△ABC中,角A,B,C的對(duì)邊分別為a,b,c,并且b=2
(1)若角A,B,C成等差數(shù)列,求△ABC外接圓的半徑;
(2)若三邊a,b,c成等差數(shù)列,求△ABC內(nèi)切圓半徑的最大值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com