
【題目】下列選項正確的為( )
A.已知直線![]() :
:![]() ,
,![]() :
:![]() ,則
,則![]() 的充分不必要條件是
的充分不必要條件是![]()
B.命題“若數列![]() 為等比數列,則數列
為等比數列,則數列![]() 為等比數列”是假命題
為等比數列”是假命題
C.棱長為![]() 正方體
正方體![]() 中,平面
中,平面![]() 與平面
與平面![]() 距離為
距離為![]()
D.已知![]() 為拋物線
為拋物線![]() 上任意一點且
上任意一點且![]() ,若
,若![]() 恒成立,則
恒成立,則![]()
【答案】ABCD
【解析】
A.分析“![]() ”與“
”與“![]() ”的互相推出情況,由此確定是否為充分不必要條件;
”的互相推出情況,由此確定是否為充分不必要條件;
B.分析特殊情況:![]() 時,
時,![]() ,由此判斷命題真假;
,由此判斷命題真假;
C.將面面距離轉化為點到面的距離,從而可求出面面距離并判斷對錯;
D.根據線段長度之間的關系列出不等式,從而可求解出![]() 的取值范圍.
的取值范圍.
A.當![]() 時,
時,![]() ,
,![]() ,顯然
,顯然![]() ;
;
當![]() 時,
時,![]() ,解得
,解得![]() ,
,
所以![]() 的充分不必要條件是
的充分不必要條件是![]() 正確;
正確;
B.當![]() 時,
時,![]() ,所以此時
,所以此時![]() 為等比數列,
為等比數列,
但![]() 不是等比數列,所以命題是假命題,故正確;
不是等比數列,所以命題是假命題,故正確;
C.如圖所示:
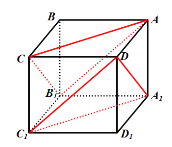
由圖可知:![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
所以平面![]() 與平面
與平面![]() 距離即為
距離即為![]() 到平面
到平面![]() 的距離,記為
的距離,記為![]() ,
,
由等體積可知: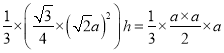 ,所以
,所以![]() ,故正確;
,故正確;
D.設![]() ,因為
,因為![]() ,所以
,所以![]() ,
,
所以![]() 且
且![]() ,所以
,所以![]() ,
,
當![]() 時顯然符合,當
時顯然符合,當![]() 時
時![]() ,所以
,所以![]() ,
,
綜上可知:![]() .故正確.
.故正確.
故選:ABCD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】我國古代數學家祖暅提出原理:“冪勢既同,則積不容異”.其中“冪”是截面積,“勢”是幾何體的高.該原理的意思是:夾在兩個平行平面間的兩個幾何體,被任一平行于這兩個平行平面的平面所截,若所截的兩個截面的面積恒相等,則這兩個幾何體的體積相等.如圖,在空間直角坐標系中的![]() 平面內,若函數
平面內,若函數![]() 的圖象與
的圖象與![]() 軸圍成一個封閉的區域
軸圍成一個封閉的區域![]() ,將區域
,將區域![]() 沿
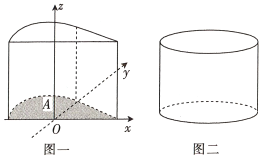
沿![]() 軸的正方向平移8個單位長度,得到幾何體如圖一,現有一個與之等高的圓柱如圖二,其底面積與區域
軸的正方向平移8個單位長度,得到幾何體如圖一,現有一個與之等高的圓柱如圖二,其底面積與區域![]() 的面積相等,則此圓柱的體積為__________.
的面積相等,則此圓柱的體積為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在原點,左焦點
的中心在原點,左焦點![]() 、右焦點
、右焦點![]() 都在
都在![]() 軸上,點
軸上,點![]() 是橢圓
是橢圓![]() 上的動點,
上的動點,![]() 的面積的最大值為
的面積的最大值為![]() ,在
,在![]() 軸上方使
軸上方使![]() 成立的點
成立的點![]() 只有一個.
只有一個.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的兩直線
的兩直線![]() ,
,![]() 分別與橢圓
分別與橢圓![]() 交于點
交于點![]() ,
,![]() 和點
和點![]() ,
,![]() ,且
,且![]() ,比較
,比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
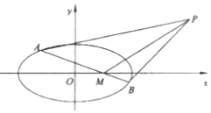
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() ,點
,點![]() 在
在![]() 軸上,過點
軸上,過點![]() 的直線交橢圓
的直線交橢圓![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
①若直線![]() 的斜率為
的斜率為![]() ,且
,且![]() ,求點
,求點![]() 的坐標;
的坐標;
②設直線![]() ,
,![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,
,![]() ,是否存在定點
,是否存在定點![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 點坐標;若不存在,請說明理由.
點坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,以等腰直角三角形ABC的斜邊BC上的高AD為折痕,把△ABD和△ACD折成互相垂直的兩個平面后,某學生得出下列四個結論:
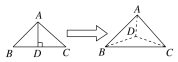
①BD⊥AC;
②△BAC是等邊三角形;
③三棱錐D-ABC是正三棱錐;
④平面ADC⊥平面ABC.
其中正確的是( )
A.①②④B.①②③
C.②③④D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2ax-![]() x2-3ln x,其中a∈R,為常數.
x2-3ln x,其中a∈R,為常數.
(1)若f(x)在x∈[1,+∞)上是減函數,求實數a的取值范圍;
(2)若x=3是f(x)的極值點,求f(x)在x∈[1,a]上的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 過點
過點![]() 與點
與點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 過定點
過定點![]() ,且斜率為
,且斜率為![]() ,若橢圓
,若橢圓![]() 上存在
上存在![]() ,
,![]() 兩點關于直線
兩點關于直線![]() 對稱,
對稱,![]() 為坐標原點,求
為坐標原點,求![]() 的取值范圍及
的取值范圍及![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知p:函數f(x)在R上是增函數,f(m2)<f(m+2)成立;q:方程![]() 1(m∈R)表示雙曲線.
1(m∈R)表示雙曲線.
(1)若p為真命題,求m的取值范圍;
(2)若p∨q為真,p∧q為假,求m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com