
【題目】已知函數(shù)![]() .
.
(1)若![]() 在定義域內(nèi)單調(diào)遞增,求
在定義域內(nèi)單調(diào)遞增,求![]() 的值;
的值;
(2)討論![]() 的零點個數(shù).
的零點個數(shù).
【答案】(1)![]() (2)若
(2)若![]() ,
,![]() 無零點;若
無零點;若![]() ,
,![]() 有兩個零點;若
有兩個零點;若![]() 或
或![]() ,
,![]() 有一個零點.
有一個零點.
【解析】
(1)求導得![]() ,設(shè)
,設(shè)![]() ,則
,則![]() 在
在![]() 上單調(diào)遞增,根據(jù)
上單調(diào)遞增,根據(jù)![]() 、
、![]() 、
、![]() 與
與![]() 分類討論,找到令
分類討論,找到令![]() 恒成立的
恒成立的![]() 的取值范圍即可得解;
的取值范圍即可得解;
(2)分為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 和
和![]() 分類討論,根據(jù)(1)求得的單調(diào)性結(jié)合零點存在性定理,即可得解.
分類討論,根據(jù)(1)求得的單調(diào)性結(jié)合零點存在性定理,即可得解.
(1)由題意得![]() 的定義域為
的定義域為![]() ,
,
![]() ,
,
設(shè)![]() ,則
,則![]() ,
,![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
若![]() ,則
,則![]() ,所以當
,所以當![]() ,
,![]() ,當
,當![]() ,
,![]() ;
;
若![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有唯一零點,設(shè)為
上有唯一零點,設(shè)為![]() ,
,
所以當![]() ,
,![]() ,當
,當![]() ,
,![]() ,當
,當![]() ,
,![]() ;
;
若![]() ,
,![]() ,所以當
,所以當![]() ,
,![]() ,當
,當![]() ,
,![]() ;
;
若![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有唯一零點,設(shè)為
上有唯一零點,設(shè)為![]() ,
,
所以當![]() ,
,![]() ,當
,當![]() ,
,![]() ,當
,當![]() ,
,![]() ;
;
綜上所述,若![]() 在其定義域內(nèi)單調(diào)遞增,則
在其定義域內(nèi)單調(diào)遞增,則![]() .
.
(2)若![]() ,
,![]() 在
在![]() 上有唯一零點
上有唯一零點![]() ;
;
由(1)知,![]() 時,
時,![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以![]() 最小值為
最小值為![]() ,
,
若![]() ,則
,則![]() ,即
,即![]() ,
,![]() 無零點;
無零點;
若![]() ,則
,則![]() ,
,![]() 有唯一零點;
有唯一零點;
若![]() ,則
,則![]() ,
,![]() ,
,![]() 在
在![]() 上有唯一零點,
上有唯一零點,
又 ![]() ,
,![]() ,
,
所以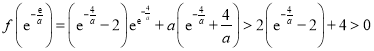 ,
,
所以![]() 在
在![]() 上有唯一零點,所以
上有唯一零點,所以![]() 在
在![]() 上有兩個零點;
上有兩個零點;
設(shè)![]() ,
,![]() ,
,![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以![]() ,即
,即![]() ,所以
,所以![]() ,所以
,所以![]() ;
;
若![]() ,當
,當![]() 時,
時,![]() ,
,
![]()
![]() ,
,
由(1)知![]() 在
在![]() 上單調(diào)遞增,所以
上單調(diào)遞增,所以![]() 在
在![]() 上有唯一零點;
上有唯一零點;
若![]() ,
,![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,
當![]() 時,
時,![]() ,
,
因為![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有唯一零點;
上有唯一零點;
綜上,若![]() ,
,![]() 無零點;若
無零點;若![]() ,
,![]() 有兩個零點;若
有兩個零點;若![]() 或
或![]() ,
,![]() 有一個零點.
有一個零點.


 步步高達標卷系列答案
步步高達標卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,側(cè)面PAD是邊長為2的等邊三角形且垂直于底![]() ,
, ![]()
![]() 是
是![]() 的中點。
的中點。
(1)證明:直線![]() 平面
平面![]() ;
;
(2)點![]() 在棱
在棱![]() 上,且直線
上,且直線![]() 與底面
與底面![]() 所成角為
所成角為![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某市為了改善居民的休閑娛樂活動場所,現(xiàn)有一塊矩形![]() 草坪如下圖所示,已知:
草坪如下圖所示,已知:![]() 米,
米,![]() 米,擬在這塊草坪內(nèi)鋪設(shè)三條小路
米,擬在這塊草坪內(nèi)鋪設(shè)三條小路![]() 、
、![]() 和
和![]() ,要求點
,要求點![]() 是
是![]() 的中點,點
的中點,點![]() 在邊
在邊![]() 上,點
上,點![]() 在邊
在邊![]() 時上,且
時上,且![]() .
.
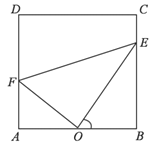
(1)設(shè)![]() ,試求
,試求![]() 的周長
的周長![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式,并求出此函數(shù)的定義域;
的函數(shù)解析式,并求出此函數(shù)的定義域;
(2)經(jīng)核算,三條路每米鋪設(shè)費用均為![]() 元,試問如何設(shè)計才能使鋪路的總費用最低?并求出最低總費用.
元,試問如何設(shè)計才能使鋪路的總費用最低?并求出最低總費用.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為響應(yīng)國家“精準扶貧、精準脫貧”的號召,某貧困縣在精準推進上下功夫,在精準扶貧上見實效.根據(jù)當?shù)貧夂蛱攸c大力發(fā)展中醫(yī)藥產(chǎn)業(yè),藥用昆蟲的使用相應(yīng)愈來愈多,每年春暖以后到寒冬前,昆蟲大量活動與繁殖,易于采取各種藥用昆蟲.已知一只藥用昆蟲的產(chǎn)卵數(shù)![]() (單位:個)與一定范圍內(nèi)的溫度
(單位:個)與一定范圍內(nèi)的溫度![]() (單位:
(單位:![]() )有關(guān),于是科研人員在
)有關(guān),于是科研人員在![]() 月份的
月份的![]() 天中隨機選取了
天中隨機選取了![]() 天進行研究,現(xiàn)收集了該種藥物昆蟲的
天進行研究,現(xiàn)收集了該種藥物昆蟲的![]() 組觀察數(shù)據(jù)如表:
組觀察數(shù)據(jù)如表:
日期 |
|
|
|
|
|
溫度 |
|
|
|
|
|
產(chǎn)卵數(shù) |
|
|
|
|
|
(1)從這![]() 天中任選
天中任選![]() 天,記這
天,記這![]() 天藥用昆蟲的產(chǎn)卵數(shù)分別為
天藥用昆蟲的產(chǎn)卵數(shù)分別為![]() 、
、![]() ,求“事件
,求“事件![]() ,
,![]() 均不小于
均不小于![]() ”的概率?
”的概率?
(2)科研人員確定的研究方案是:先從這![]() 組數(shù)據(jù)中任選
組數(shù)據(jù)中任選![]() 組,用剩下的
組,用剩下的![]() 組數(shù)據(jù)建立線性回歸方程,再對被選取的
組數(shù)據(jù)建立線性回歸方程,再對被選取的![]() 組數(shù)據(jù)進行檢驗.
組數(shù)據(jù)進行檢驗.
①若選取的是![]() 月
月![]() 日與
日與![]() 月
月![]() 日這
日這![]() 組數(shù)據(jù),請根據(jù)
組數(shù)據(jù),請根據(jù)![]() 月
月![]() 日、
日、![]() 日和
日和![]() 日這三組數(shù)據(jù),求出
日這三組數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程?
的線性回歸方程?
②若由線性回歸方程得到的估計數(shù)據(jù)與所選出的檢驗數(shù)據(jù)的差的絕對值均不超過![]() 個,則認為得到的線性回歸方程是可靠的,試問①中所得的線性回歸方程是否可靠?
個,則認為得到的線性回歸方程是可靠的,試問①中所得的線性回歸方程是否可靠?
附公式:![]() ,
,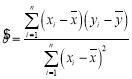 .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() 平面
平面![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點.
的中點.
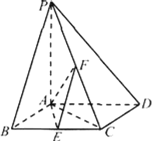
(1)證明:![]() ;
;
(2)取![]() ,若
,若![]() 為
為![]() 上的動點,
上的動點,![]() 與面
與面![]() 所成最大角的正弦值為
所成最大角的正弦值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨著時代的發(fā)展,A城市的競爭力、影響力日益卓著,這座創(chuàng)新引領(lǐng)型城市有望踏上向“全球城市”發(fā)起“沖擊”的新征程.A城市的活力與包容無不吸引著無數(shù)懷揣夢想的年輕人前來發(fā)展,目前A城市的常住人口大約為1300萬.近日,某報社記者作了有關(guān)“你來A城市發(fā)展的理由”的調(diào)查問卷,參與調(diào)查的對象年齡層次在25~44歲之間.收集到的相關(guān)數(shù)據(jù)如下:
來A城市發(fā)展的理由 | 人數(shù) | 合計 | |
自然環(huán)境 | 1.森林城市,空氣清新 | 200 | 300 |
2.降水充足,氣候怡人 | 100 | ||
人文環(huán)境 | 3.城市服務(wù)到位 | 150 | 700 |
4.創(chuàng)業(yè)氛圍好 | 300 | ||
5.開放且包容 | 250 | ||
合計 | 1000 | 1000 | |
(1)根據(jù)以上數(shù)據(jù),預測400萬25~44歲年齡的人中,選擇“創(chuàng)業(yè)氛圍好”來A城市發(fā)展的有多少人;
(2)從所抽取選擇“自然環(huán)境”作為來A城市發(fā)展的理由的300人中,利用分層抽樣的方法抽取6人,從這6人中再選取3人發(fā)放紀念品.求選出的3人中至少有2人選擇“森林城市,空氣清新”的概率;
(3)在選擇“自然環(huán)境”作為來A城市發(fā)展的理由的300人中有100名男性;在選擇“人文環(huán)境”作為來A城市發(fā)展的理由的700人中有400名男性;請?zhí)顚懴旅?/span>![]() 列聯(lián)表,并判斷是否有
列聯(lián)表,并判斷是否有![]() 的把握認為性別與“自然環(huán)境”或“人文環(huán)境”的選擇有關(guān)?
的把握認為性別與“自然環(huán)境”或“人文環(huán)境”的選擇有關(guān)?
自然環(huán)境 | 人文環(huán)境 | 合計 | |
男 | |||
女 | |||
合計 |
附: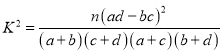 ,
,![]() .
.
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=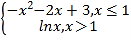 ,若關(guān)于x的方程f(x)=kx-
,若關(guān)于x的方程f(x)=kx-![]() 恰有4個不相等的實數(shù)根,則實數(shù)k的取值范圍是( )
恰有4個不相等的實數(shù)根,則實數(shù)k的取值范圍是( )
A.![]() B.
B.![]()
C.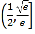 D.
D.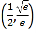
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知定點![]() 、
、![]() ,直線
,直線![]() 、
、![]() 相交于點
相交于點![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() ,記動點
,記動點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)已知定點![]() ,
,![]() ,過點
,過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點 ,則直線
兩點 ,則直線![]() 與
與![]() 斜率之積是否為定值,若是求出定值;若不是請說明理由.
斜率之積是否為定值,若是求出定值;若不是請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com