【題目】已知函數(shù)
.
（1）利用絕對值及分段函數(shù)知識，將函數(shù)
的解析式寫成分段函數(shù)；
（2）在給出的坐標系中畫出的圖象，并根據(jù)圖象寫出函數(shù)的單調(diào)區(qū)間和值域.
【答案】（1）
------3分
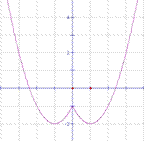
（2）圖象如右圖所示 --------------6分
單調(diào)增區(qū)間為
單調(diào)減區(qū)間為
--------------9分
值域為：
【解析】
本試題主要是考查了函數(shù)圖像以及函數(shù)單調(diào)性的運用。
（1）首先去掉絕對值符號，然后。
（2）利用函數(shù)解析式作圖
（3）根據(jù)圖像觀察可知函數(shù)的單調(diào)區(qū)間和值域。
解：（1）------3分
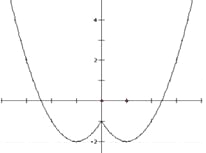
（2）圖象如右圖所示
--------------6分
單調(diào)增區(qū)間為
單調(diào)減區(qū)間為--------------9分
值域為：--------------12分
名校課堂系列答案科目：高中數(shù)學 來源： 題型：
【題目】在外接圓直徑為1的△ABC中，角A，B，C的對邊分別為a，b，c，設向量 
=（a，cosB）， 
=（b，cosA），且 ∥ ， ≠ ．
（1）求sinA+sinB的取值范圍；
（2）若abx=a+b，試確定實數(shù)x的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知在直角坐標系
中，曲線
的參數(shù)方程為
（
為參數(shù)）；在極坐標系（與直角坐標系取相同的單位長度，且以原點
為極點，以
軸正半軸為極軸）中，直線
的方程為
.
（1）求曲線的普通方程和直線的直角坐標方程；
（2）求直線被曲線截得的弦長.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，平面中兩條直線
和
相交于點O，對于平面上任意一點M，若x，y分別是M到直線和的距離，則稱有序非負實數(shù)對（x，y）是點M的“距離坐標”．已知常數(shù)p≥0，q≥0，給出下列三個命題：
①若p=q=0，則“距離坐標”為（0，0）的點有且只有1個；
②若pq=0，且p+q≠0，則“距離坐標”為（p，q）的點有且只有2個；
③若pq≠0則“距離坐標”為（p，q）的點有且只有4個．
上述命題中，正確命題的是______．（寫出所有正確命題的序號）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】數(shù)列
中，
在直線
．
（1）求數(shù)列{an}的通項公式；
（2）令
，數(shù)列
的前n項和為
．
（ⅰ）求；
（ⅱ）是否存在整數(shù)λ
，使得不等式(－1)nλ＜
(n∈N
)恒成立？若存在，求出λ的取值的集合；若不存在，請說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】學校對校園進行綠化，移栽香樟和桂花兩種大樹各2株，若香樟的成活率為
，桂花的成活率為
，假設每棵樹成活與否是相互獨立的.求：
（Ⅰ）兩種樹各成活一株的概率；
（Ⅱ）設ξ表示兩種樹成活的總株數(shù)，求ξ的分布列及數(shù)學期望.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】因金融危機，某公司的出口額下降，為此有關專家提出兩種促進出口的方案，每種方案都需要分兩年實施。若實施方案一，預計第一年可以使出口額恢復到危機前的
倍、
倍、
倍的概率分別為
、、
；第二年可以使出口額為第一年的
倍、倍的概率分別為
、。若實施方案二，預計第一年可以使出口額恢復到危機前的
倍、倍、倍的概率分別為
、、；第二年可以使出口額為第一年的倍、倍的概率分別為、
。實施每種方案第一年與第二年相互獨立。令
表示方案
實施兩年后出口額達到危機前的倍數(shù)。
（1）寫出
的分布列；
（2）實施哪種方案，兩年后出口額超過危機前出口額的概率更大？
（3）不管哪種方案，如果實施兩年后出口額達不到、恰好達到、超過危機前出口額，預計利潤分別為
萬元、
萬元、
萬元，問實施哪種方案的平均利潤更大？
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
