【題目】已知函數f（x）=sin2x+acosx+x在點x= 
處取得極值．
（1）求實數a的值；
（2）當x∈[﹣ ， 
]時，求函數f（x）的最大值．
【答案】
（1）解：f（x）=sin2x+acosx+x，
f′（x）=2cos2x﹣asinx+1，
f′（ 
）=2cos 
﹣asin +1=0，
解得：a=4
（2）解：由（1）得：f（x）=sin2x+4cosx+x，
f′（x）=2cos2x﹣4sinx+1=2﹣4sin2x﹣4sinx+1=﹣（2sinx+1）2+4，
令f′（x）＞0，解得：﹣ ＜x＜ 或 
＜x＜ 
，
令f′（x）＜0，解得： ＜x＜ ，
∴f（x）在[﹣ ， ）遞增，在（ ， ）遞減，在（ ， ）遞增，
∴f（x）的最大值是f（ ）或f（ ），
而f（ ）= 
﹣2+ ＜f（ ）= 
+ ，
故f（x）的最大值是f（ ）= +
【解析】（1）求出函數的導數，根據f′（ ）=0，求出a的值即可；（2）求出函數的導數，解關于導函數的不等式，求出函數的單調區間，從而求出函數的最大值即可．
【考點精析】關于本題考查的利用導數研究函數的單調性和函數的最大(小)值與導數，需要了解一般的,函數的單調性與其導數的正負有如下關系： 在某個區間
內，(1)如果
，那么函數
在這個區間單調遞增；(2)如果
，那么函數
在這個區間單調遞減；求函數在
上的最大值與最小值的步驟：（1）求函數在內的極值；（2）將函數的各極值與端點處的函數值
，
比較，其中最大的是一個最大值，最小的是最小值才能得出正確答案．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】某地電影院為了了解當地影迷對快要上映的一部電影的票價的看法，進行了一次調研，得到了票價x(單位：元)與渴望觀影人數y(單位：萬人)的結果如下表：
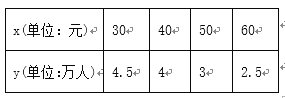
(1)請根據上表提供的數據，用最小二乘法求出y關于x的線性回歸方程；
(2)根據(1)中求出的線性回歸方程，若票價定為70元，預測該電影院渴望觀影人數．附：回歸直線的斜率和截距的最小二乘法估計公式分別為：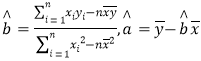
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種植園在芒果臨近成熟時，隨機從一些芒果樹上摘下100個芒果，其質量分別在
，
，
，
，
，
（單位：克）中，經統計得頻率分布直方圖如圖所示.
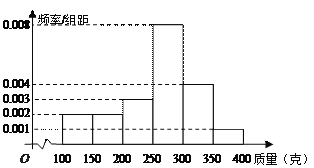
(1) 經計算估計這組數據的中位數；
(2)現按分層抽樣從質量為，的芒果中隨機抽取
個，再從這個中隨機抽取
個，求這個芒果中恰有
個在內的概率.
（3）某經銷商來收購芒果，以各組數據的中間數代表這組數據的平均值，用樣本估計總體，該種植園中還未摘下的芒果大約還有
個，經銷商提出如下兩種收購方案：
A：所以芒果以
元/千克收購；
B：對質量低于
克的芒果以
元/個收購，高于或等于克的以元/個收購.
通過計算確定種植園選擇哪種方案獲利更多？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，內角A，B，C所對的邊分別為a、b、c，已知a=csinB+bcosC．
（1）求A+C的值；
（2）若b= 
，求△ABC面積的最值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知圓O外有一點P，作圓O的切線PM，M為切點，過PM的中點N，作割線NAB，交圓于A，B兩點，連接PA并延長，交圓O于點C，連續PB交圓O于點D，若MC=BC．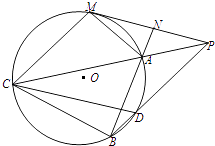 
（1）求證：△APM∽△ABP；
（2）求證：四邊形PMCD是平行四邊形．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}的前n項和為Sn ， a1=1，an+1=2Sn+1（n∈N*），等差數列{bn}滿足b3=3，b5=9．
（1）分別求數列{an}，{bn}的通項公式；
（2）設Cn= 
（n∈N*），求證Cn+1＜Cn 
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
