
【題目】已知![]() 的圖象在
的圖象在![]() 處的切線與直線
處的切線與直線![]() 平行.
平行.
(1)求函數![]() 的極值;
的極值;
(2)若![]() ,
,![]() ,
,![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)極大值為![]() ,無極小值;(2)
,無極小值;(2)![]() ,
,![]() .
.
【解析】
(1)可利用導數的幾何意義求出a的值,然后利用函數導數得到函數的單調性,求得函數的極值;
(2)所給不等式含有兩個變量,通過變形使兩個變量![]() 分別在不等式兩側,然后構造新函數g(x),轉化為函數的單調性即可求解m的范圍.
分別在不等式兩側,然后構造新函數g(x),轉化為函數的單調性即可求解m的范圍.
(1)![]() 的導數為
的導數為![]() ,
,
可得![]() 的圖象在
的圖象在![]() ,
,![]() (1)
(1)![]() 處的切線斜率為
處的切線斜率為![]() ,
,
由切線與直線![]() 平行,可得
平行,可得![]() ,
,
即![]() ,
,![]() ,
,
![]() ,
,
由![]() ,可得
,可得![]() ,由
,由![]() ,可得
,可得![]() ,
,
則![]() 在
在![]() 遞增,在
遞增,在![]() 遞減,
遞減,
可得![]() 在
在![]() 處取得極大值為
處取得極大值為![]() ,無極小值;
,無極小值;
(2)可設![]() ,若
,若![]() ,
,![]() ,
,
![]() ,可得
,可得![]() ,
,
即有![]() ,
,
設![]() 在
在![]() 為增函數,
為增函數,
即有![]() 對
對![]() 恒成立,
恒成立,
可得![]() 在
在![]() 恒成立,
恒成立,
由![]() 的導數為
的導數為![]() 得:
得:
當![]() ,可得
,可得![]() ,
,
![]() 在
在![]() 遞減,在
遞減,在![]() ,
,![]() 遞增,
遞增,
即有![]() 在
在![]() 處取得極小值,且為最小值
處取得極小值,且為最小值![]() ,
,
可得![]() ,
,
解得![]() ,
,
則實數![]() 的取值范圍是
的取值范圍是![]() ,
,![]() .
.


科目:高中數學 來源: 題型:
【題目】某保險公司對一個擁有20000人的企業推出一款意外險產品,每年每位職工只要交少量保費,發生意外后可一次性獲得若干賠償金,保險公司把企業的所有崗位共分為![]() 三類工種,從事這三類工種的人數分別為12000,6000,2000,由歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付概率):
三類工種,從事這三類工種的人數分別為12000,6000,2000,由歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付概率):
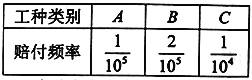
已知![]() 三類工種職工每人每年保費分別為25元、25元、40元,出險后的賠償金額分別為100萬元、100萬元、50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
三類工種職工每人每年保費分別為25元、25元、40元,出險后的賠償金額分別為100萬元、100萬元、50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
(1)求保險公司在該業務所或利潤的期望值;
(2)現有如下兩個方案供企業選擇:
方案1:企業不與保險公司合作,職工不交保險,出意外企業自行拿出與保險公司提供的等額賠償金賠償付給意外職工,企業開展這項工作的固定支出為每年12萬元;
方案2:企業與保險公司合作,企業負責職工保費的70%,職工個人負責保費的30%,出險后賠償金由保險公司賠付,企業無額外專項開支.
請根據企業成本差異給出選擇合適方案的建議.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】曲一中某研究性學習小組對學習數學的練習時間與進步率的關系進行研究,他們分別記錄了同班5個同學一周內的學習時間與周測成績進步率,得到如下資料.

(1)從5個同學中任選2個,記其進步率分別為![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2)若進步率![]() 與學習時間
與學習時間![]() 服從線性關系,求出
服從線性關系,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)在這5個同學中任取3個,其中進步率超過25的有![]() 個同學,求
個同學,求![]() 的數學期望.
的數學期望.
參考公式:回歸直線方程是![]() ,其中
,其中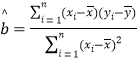
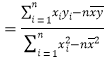
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是橢圓
是橢圓![]() :
:![]() (
(![]() )與拋物線
)與拋物線![]() :
:![]() 的一個公共點,且橢圓與拋物線具有一個相同的焦點
的一個公共點,且橢圓與拋物線具有一個相同的焦點![]() .
.
(Ⅰ)求橢圓![]() 及拋物線
及拋物線![]() 的方程;
的方程;
(Ⅱ)設過![]() 且互相垂直的兩動直線
且互相垂直的兩動直線![]() ,
,![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,
兩點,![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超強臺風登陸海南省.據統計,本次臺風造成全省直接經濟損失119.52億元,適逢暑假,小明調查住在自己小區的50戶居民由于臺風造成的經濟損失,作出如下頻率分布直方圖:
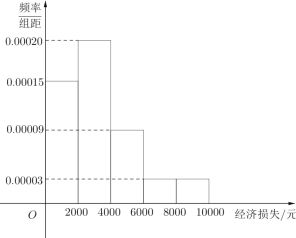
| 經濟損失4000元以下 | 經濟損失4000元以上 | 合計 |
捐款超過500元 | 30 | ||
捐款低于500元 | 6 | ||
合計 |
臺風后區委會號召小區居民為臺風重災區捐款,小明調查的50戶居民捐款情況如上表,在表格空白處填寫正確數字,并說明是否有![]() 以上的把握認為捐款數額是否多于或少于500元和自身經濟損失是否到4000元有關?
以上的把握認為捐款數額是否多于或少于500元和自身經濟損失是否到4000元有關?
附:臨界值表
| 2.072 | 2.706 | 3.841 | 5.024 | 6635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
參考公式: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的單調區間;
(Ⅱ)已知f(x)在x=1處取得極大值.求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com