
【題目】已知在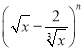 的展開式中,第5項(xiàng)的系數(shù)與第3項(xiàng)的系數(shù)之比是56:3.
的展開式中,第5項(xiàng)的系數(shù)與第3項(xiàng)的系數(shù)之比是56:3.
(1)求展開式中的所有有理項(xiàng);
(2)求展開式中系數(shù)絕對值最大的項(xiàng).
(3)求![]() 的值.
的值.
【答案】(1)T1=x5和T7=13400 ,(2)![]() ,(3)
,(3)![]() .
.
【解析】試題分析:(1)求二項(xiàng)展開式中特定項(xiàng),關(guān)鍵在從通項(xiàng)出發(fā),找尋對應(yīng)等量關(guān)系. 由![]() 解得n=10,因?yàn)橥?xiàng):
解得n=10,因?yàn)橥?xiàng): 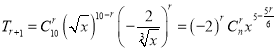 ,當(dāng)5﹣
,當(dāng)5﹣![]() 為整數(shù),r可取0,6,于是有理項(xiàng)為T1=x5和T7=13400,(2)求展開式中系數(shù)絕對值最大的項(xiàng),通過列不等式解決. 設(shè)第r+1項(xiàng)系數(shù)絕對值最大,則
為整數(shù),r可取0,6,于是有理項(xiàng)為T1=x5和T7=13400,(2)求展開式中系數(shù)絕對值最大的項(xiàng),通過列不等式解決. 設(shè)第r+1項(xiàng)系數(shù)絕對值最大,則![]() ,解得
,解得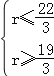 ,于是r只能為7,所以系數(shù)絕對值最大的項(xiàng)為
,于是r只能為7,所以系數(shù)絕對值最大的項(xiàng)為![]() ,(3)本題是二項(xiàng)式定理的逆向應(yīng)用,關(guān)鍵將式子轉(zhuǎn)化符合二項(xiàng)展開式的特征.
,(3)本題是二項(xiàng)式定理的逆向應(yīng)用,關(guān)鍵將式子轉(zhuǎn)化符合二項(xiàng)展開式的特征. ![]()
![]()
![]()
![]()
(1)由![]() 解得n=10 (2分)
解得n=10 (2分)
因?yàn)橥?xiàng): 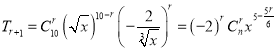 (3分)
(3分)
當(dāng)5﹣![]() 為整數(shù),r可取0,6 (4分)
為整數(shù),r可取0,6 (4分)
展開式是常數(shù)項(xiàng),于是有理項(xiàng)為T1=x5和T7=13400 (6分)
(2)設(shè)第r+1項(xiàng)系數(shù)絕對值最大,則![]() (8分)
(8分)
注:等號不寫扣(1分)
解得 ,于是r只能為7 (10分)
,于是r只能為7 (10分)
所以系數(shù)絕對值最大的項(xiàng)為![]() (11分)
(11分)
(3)![]()
![]()
![]() 13分
13分
![]() .16分
.16分



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
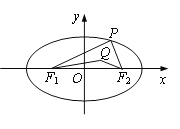
【題目】在平面直角坐標(biāo)系xOy中,已知橢圓![]() :
: ![]() 的左,右焦點(diǎn)分別為
的左,右焦點(diǎn)分別為![]() ,
, ![]() .點(diǎn)
.點(diǎn)![]() 是橢圓
是橢圓![]() 在
在![]() 軸上方的動點(diǎn),且△
軸上方的動點(diǎn),且△![]() 的周長為16.
的周長為16.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)點(diǎn)![]() 到△
到△![]() 三邊的距離均相等.
三邊的距離均相等.
①當(dāng)![]() 時,求點(diǎn)
時,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
②求證:點(diǎn)![]() 在定橢圓上.
在定橢圓上.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某醫(yī)療研究所開發(fā)一種新藥,如果成人按規(guī)定的劑量服用,據(jù)監(jiān)測:服藥后每毫升血液中的含藥量y與時間t之間近似滿足如圖所示的曲線.

(1)寫出服藥后y與t之間的函數(shù)關(guān)系式;
(2)據(jù)測定,每毫升血液中含藥量不少于4 μg時治療疾病有效,假若某病人一天中第一次服藥為上午7:00,問:一天中怎樣安排服藥時間(共4次)效果最佳?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在空間四邊形ABCD中,AB=CD,AB與CD成30°角,E,F分別為BC,AD的中點(diǎn),求EF與AB所成的角.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 與圓
與圓![]()
![]() 的公共點(diǎn)的軌跡為曲線
的公共點(diǎn)的軌跡為曲線![]() ,且曲線
,且曲線![]() 與
與![]() 軸的正半軸相交于點(diǎn)
軸的正半軸相交于點(diǎn)![]() .若曲線
.若曲線![]() 上相異兩點(diǎn)
上相異兩點(diǎn)![]() 滿足直線
滿足直線![]() 的斜率之積為
的斜率之積為![]() .
.
(1)求![]() 的方程;
的方程;
(2)證明直線![]() 恒過定點(diǎn),并求定點(diǎn)的坐標(biāo).
恒過定點(diǎn),并求定點(diǎn)的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=(-x2+x-1)ex,其中e是自然對數(shù)的底數(shù).
(1)求曲線f(x)在點(diǎn)(1,f(1))處的切線;
(2)若方程f(x)=![]() x3+
x3+![]() x2+m有3個不同的根,求實(shí)數(shù)m的取值范圍.
x2+m有3個不同的根,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司從1999年的年產(chǎn)值100萬元,增加到10年后2009年的500萬元,如果每年產(chǎn)值增長率相同,則每年的平均增長率是多少?(ln(1+x)≈x,lg2=0.3,ln10=2.30)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司生產(chǎn)電飯煲,每年需投入固定成本40萬元,每生產(chǎn)1萬件還需另投入16萬元的變動成本,設(shè)該公司一年內(nèi)共生產(chǎn)電飯煲![]() 萬件并全部銷售完,每一萬件的銷售收入為
萬件并全部銷售完,每一萬件的銷售收入為![]() 萬元,且
萬元,且![]() (
(![]() ),該公司在電飯煲的生產(chǎn)中所獲年利潤為
),該公司在電飯煲的生產(chǎn)中所獲年利潤為![]() (萬元),(注:利潤=銷售收入-成本)
(萬元),(注:利潤=銷售收入-成本)
(1)寫出年利潤![]() (萬元)關(guān)于年產(chǎn)量
(萬元)關(guān)于年產(chǎn)量![]() (萬件)的函數(shù)解析式,并求年利潤的最大值;
(萬件)的函數(shù)解析式,并求年利潤的最大值;
(2)為了讓年利潤![]() 不低于2360萬元,求年產(chǎn)量
不低于2360萬元,求年產(chǎn)量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,一個樹形圖依據(jù)下列規(guī)律不斷生長,1個空心圓點(diǎn)到下一行僅生長出1個實(shí)心圓點(diǎn),1個實(shí)心圓點(diǎn)到下一行生長出1個實(shí)心圓點(diǎn)和1個空心圓點(diǎn),則第11行的實(shí)心圓點(diǎn)的個數(shù)是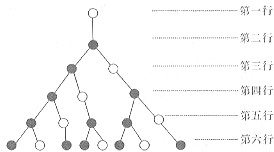
A. 21 B. 34 C. 55 D. 89
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com