甲、乙二人平時跑步路程與時間的關(guān)系以及百米賽跑路程和時間的關(guān)
系分別如圖①、②所示.問:
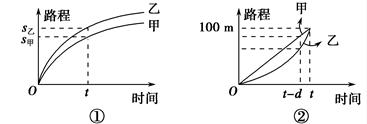
(1)甲、乙二人平時跑步哪一個跑得快?
(2)甲、乙二人百米賽跑,快到終點時,誰跑得快(設(shè)Δ
s為
s的增量)?
(1)由題圖①在(0,
t]時間段內(nèi),甲、乙跑過的路程
s甲<
s乙,故有
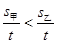
即在任一時間段(0,
t]內(nèi),甲的平均速度小于乙的平均速度,所以乙比甲跑得快.
(2)由題圖②知,在終點附近[
t-
d,
t)時間段內(nèi),路程增量Δ
s乙>Δ
s甲,所以
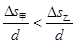
即快到終點時,乙的平均速度大于甲的平均速度,所以乙比甲跑得快
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知函數(shù)
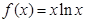
,
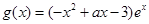
(a為實數(shù)).
(1) 當(dāng)a=5時,求函數(shù)
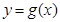
在
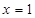
處的切線方程;
(2) 求
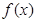
在區(qū)間
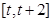
(
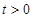
)上的最小值;
(3) 若存在兩不等實根
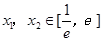
,使方程
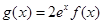
成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知函數(shù)
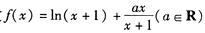
(1)當(dāng)a=2時,求函數(shù)y=f(x)的圖象在x=0處的切線方程;
(2)判斷函數(shù)f(x)的單調(diào)性;
(3)求證:
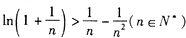
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知
a,
b∈R,函數(shù)
f(
x)=
a+ln(
x+1)的圖象與
g(
x)=
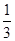 x3
x3-
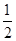 x2
x2+
bx的圖象在交點(0,0)處有公共切線.
(1)證明:不等式
f(
x)≤
g(
x)對一切
x∈(-1,+∞)恒成立;
(2)設(shè)-1<
x1<
x2,當(dāng)
x∈(
x1,
x2)時,證明:
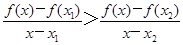
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
設(shè)f(x)=ln(x
2+1),g(x)=
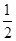
x
2-
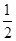
.
(1)求F(x)=f(x)-g(x)的單調(diào)區(qū)間,并證明對[-1,1]上的任意x
1,x
2,x
3,都有F(x
1)+F(x
2)>F(x
3);
(2)將y=f(x)的圖像向下平移a(a>0)個單位,同時將y=g(x)的圖像向上平移b(b>0)個單位,使它們恰有四個交點,求

的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知函數(shù)
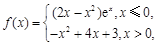
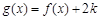
,若函數(shù)
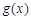
恰有兩個不同的零點,則實數(shù)
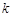
的取值范圍為
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
設(shè)
f0(
x)=cos
x,
f1(
x)=
f0′(
x),
f2(
x)=
f1′(
x),…,
fn+1(
x)=
fn′(
x),
n∈
N,則
f2 011(
x)等于 ( ).
| A.sin x | B.-sin x |
| C.cos x | D.-cos x |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知定義域為R的奇函數(shù)
f(
x)的導(dǎo)函數(shù)為
f′(
x),當(dāng)
x≠0時,
f′(
x)+
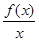
>0,若
a=
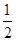 f
f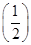
,
b=-2
f(-2),
c=ln
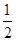 f
f(ln 2),則下列關(guān)于
a,
b,
c的大小關(guān)系正確的是( )
| A.a>b>c | B.a>c>b |
| C.c>b>a | D.b>a>c |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
若函數(shù)
f(
x)=cos
2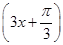
,則
f′
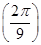
=________.
查看答案和解析>>


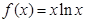 ,
,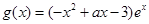 (a為實數(shù)).
(a為實數(shù)).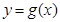 在
在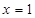 處的切線方程;
處的切線方程;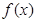 在區(qū)間
在區(qū)間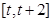 (
(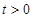 )上的最小值;
)上的最小值;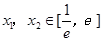 ,使方程
,使方程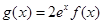 成立,求實數(shù)a的取值范圍.
成立,求實數(shù)a的取值范圍.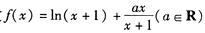
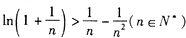
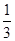 x3-
x3-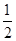 x2+bx的圖象在交點(0,0)處有公共切線.
x2+bx的圖象在交點(0,0)處有公共切線.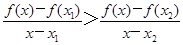 .
.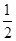 x2-
x2-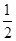 .
. 的取值范圍.
的取值范圍.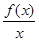 >0,若a=
>0,若a=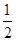 f
f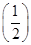 ,b=-2f(-2),c=ln
,b=-2f(-2),c=ln 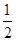 f(ln 2),則下列關(guān)于a,b,c的大小關(guān)系正確的是( )
f(ln 2),則下列關(guān)于a,b,c的大小關(guān)系正確的是( )