【題目】如圖，在四棱錐P ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分別為CD和PC的中點．
求證：(1) BE∥平面PAD；
(2) 平面BEF⊥平面PCD.
【答案】（1）見解析；（2）見解析.
【解析】試題分析：(1) 平面
平面
且
,由面面垂直的性質定理可得
底面
.(2) 可證
為平行四邊形,得
∥
,根據線面平行的判定定理證得
∥平面
.(3)由面面垂直的性質定理可得
平面
或證
, 
根據線面垂直的判定定理證
平面
可得
即
,依題意可得
為矩形,可得
,根據線面垂直的判定定理可得
平面
,從而可得平面
⊥平面
.
試題解析：證明 (1)平面
平面
.
又平面
平面
，且
.∴
底面
. 4分
(2)∵
∥
， 
， 
為
的中點，
∴
∥
，且
.∴
為平行四邊形．∴
∥
.
又∵BE平面PAD，AD平面PAD，∴
∥平面
. 8分
(3)∵
，且四邊形
為平行四邊形．
∴
， 
.
由(1)知
底面
，則
，
∴
平面
，從而
，
又
分別為
的中點，
∴
∥
，故
.
由
， 
在平面
內，且
，∴
平面
∴平面
⊥平面
. 12分
小博士期末闖關100分系列答案
名校名師培優作業本加核心試卷系列答案科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy 中，已知圓C的參數方程為 
（φ為參數）．以坐標原點為極點，x軸正半軸為極軸建立極坐標系．
（1）求圓的極坐標方程；
（2）直線l的極坐方程是 
，射線OM：θ= 
與圓的交點為O，P，與直線l的交點為Q，求線段PQ的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，平面ABCD⊥平面ABEF，四邊形ABCD是正方形，四邊形ABEF是矩形，AF＝
AD＝a，G是EF的中點．
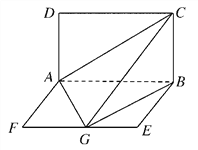
(1)求證：平面AGC⊥平面BGC；
(2)求GB與平面AGC所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題錯誤的是 （ ）
A. 如果平面
平面
，那么平面
內一定存在直線平行于平面
B. 如果平面
不垂直平面
，那么平面
內一定不存在直線垂直于平面
C. 如果平面
平面
，平面
平面
，且
，那么
D. 如果平面
平面
，那么平面
內所有直線都垂直于平面
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在二項式（ 
+ 
）n展開式中，前三項的系數成等差數列． 求：（1）展開式中各項系數和；
【答案】解：由題意得2 
× 
=1+ 
× 
，
化為：n2﹣9n+8=0，解得n=1（舍去）或8．
∴n=8．
在 
中，令x=1，可得展開式中各項系數和= 
= 
．
（1）展開式中系數最大的項．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某縣農民年均收入服從μ＝500元，σ＝20元的正態分布，求：
(1)此縣農民的年均收入在500～520元之間的人數的百分比；
(2)此縣農民的年均收入超過540元的人數的百分比．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知a＜﹣1，函數f（x）=|x3﹣1|+x3+ax（x∈R）．
（Ⅰ）求函數f（x）的最小值；
（Ⅱ）已知存在實數m，n（m＜n≤1），對任意t0∈（m，n），總存在兩個不同的t1 ， t2∈（1，+∞），
使得f（t0）﹣2=f（t1）=f（t2），求證： 
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
