【題目】計算
（1）已知f（x）=（x2+2x）ex ， 求f′（﹣1）；
（2）∫ 
cos2 
dx．
期末復習檢測系列答案
超能學典單元期中期末專題沖刺100分系列答案
黃岡360度定制密卷系列答案
陽光考場單元測試卷系列答案
名校聯盟沖刺卷系列答案科目：高中數學 來源： 題型：
【題目】平面上，點A、C為射線PM上的兩點，點B、D為射線PN上兩點，則有
（其中S△PAB、S△PCD分別為△PAB、△PCD的面積）；空間中，點A、C為射線PM上的兩點，點B、D為射線PN上的兩點，點E、F為射線PL上的兩點，則有
=___________.（其中VP-ABE、VP-CDF分別為四面體P-ABE、P-CDF的體積）。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數 
，其反函數為y=g（x）．
（1）若g（mx2+2x+1）的定義域為R，求實數m的取值范圍；
（2）當x∈[﹣1，1]時，求函數y=[f（x）]2﹣2af（x）+3的最小值h（a）；
（3）是否存在實數m＞n＞2，使得函數y=h（x）的定義域為[n，m]，值域為[n2 ， m2]，若存在，求出m、n的值；若不存在，則說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數 
+cos2x+a（a∈R，a為常數）． （Ⅰ）求函數的最小正周期；
（Ⅱ）求函數的單調遞減區間；
（Ⅲ）若 
時，f（x）的最小值為﹣2，求a的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設 
= 
， 
=（4sinx，cosx﹣sinx），f（x）= ．
（1）求函數f（x）的解析式；
（2）已知常數ω＞0，若y=f（ωx）在區間 
是增函數，求ω的取值范圍；
（3）設集合A= 
，B={x||f（x）﹣m|＜2}，若AB，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】大學生趙敏利用寒假參加社會實踐，對機械銷售公司7月份至11月份銷售某種機械配件的銷售量及銷售單價進行了調查，銷售單價x元和銷售量y件之間的一組數據如表所示：
月份 | 7 | 8 | 9 | 10 | 11 |
銷售單價x元 | 9 | 9.5 | 10 | 10.5 | 11 |
銷售量y件 | 11 | 10 | 8 | 6 | 5 |
（1）根據7至11月份的數據，求出y關于x的回歸直線方程；
（2）預計在今后的銷售中，銷售量與銷售單價仍然服從（1）中的關系，若該種機器配件的成本是2.5元/件，那么該配件的銷售單價應定為多少元才能獲得最大利潤？ 參考公式：回歸直線方程 
=b 
+a，其中b=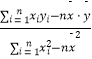 
．
參考數據： 
=392， 
=502.5．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f（x）是定義在R上的奇函數，當x＞0時，f′（x）sinx+f（x）cosx＞0且f（ 
）=1，則f（x）sinx≤1的整數解的集合為 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
