
橢圓C的中心為原點, 右焦點F(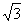 ,0), 以短軸的兩端點及F為頂點的三角形恰為等邊三角形.
,0), 以短軸的兩端點及F為頂點的三角形恰為等邊三角形.
(1)求橢圓C的標(biāo)準(zhǔn)方程;
(2)過橢圓C內(nèi)的一點P(0,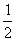 )作直線l交橢圓C于M、 N,求MN中點Q的軌跡方程;
)作直線l交橢圓C于M、 N,求MN中點Q的軌跡方程;
(3)在(2)條件下,求△OMN的面積最大值.
(1)設(shè)橢圓C的標(biāo)準(zhǔn)方程為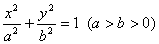 ,
,
∵ 右焦點為F(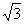 ,0) ∴
,0) ∴ 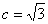
又∵ △B1FB2為正三角形 ∴ 
結(jié)合  得
得  ,
,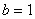
∴ 橢圓C的標(biāo)準(zhǔn)方程是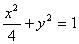 ………………………………… 4分
………………………………… 4分
(2)設(shè)Q(x,y),M(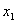 ,
, ),N(
),N( ,
,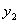 )
)
當(dāng)直線l的斜率存在時,直線l的方程為
代入 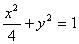 得
得 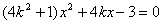
∴  ,
,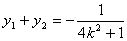 …………………… 6分
…………………… 6分
∴ 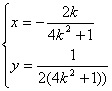
消去k得 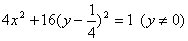 …………………………… 8分
…………………………… 8分
又∵ k不存在時,點Q為(0,0)也滿足上述方程,
∴ 線段MN的中點Q的軌跡方程是  ……… 9分
……… 9分
(3)由(2)知,M(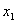 ,
, ),N(
),N( ,
,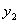 ),直線l的方程為
),直線l的方程為
代入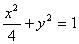 得
得 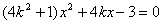
∴  ,
,
∴ 
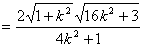 ………………………………………………… 11分
………………………………………………… 11分
又∵ 原點O到直線l的距離為
∴ 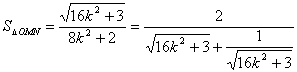 ……………… 12分
……………… 12分
設(shè)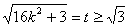
∴ 
∴ △OMN面積的最大值為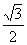 ……………………………………… 14分
……………………………………… 14分


 黎明文化寒假作業(yè)系列答案
黎明文化寒假作業(yè)系列答案 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
| ||
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 2 |
| y2 |
| 16 |
| x2 |
| 2 |
| y2 |
| 16 |
| x2 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
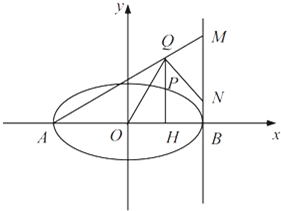 (2013•深圳一模)已知橢圓C 的中心為原點O,焦點在x 軸上,離心率為
(2013•深圳一模)已知橢圓C 的中心為原點O,焦點在x 軸上,離心率為
| ||
| 2 |
| ||
| 2 |
| PQ |
| HP |
| BM |
| BN |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| OA |
| OB |
| 1 |
| 2 |
| PA |
| PB |
| PF |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| x2 |
| 4 |
| y2 |
| 8 |
| 2 |
| x2 |
| 2 |
| x2 |
| 2 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com