
【題目】已知函數(shù)![]() .
.
(1)若![]() ,求函數(shù)
,求函數(shù)![]() 的單調(diào)遞減區(qū)間;
的單調(diào)遞減區(qū)間;
(2)若![]() ,求函數(shù)
,求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值;
上的最大值;
(3)若![]() 在區(qū)間
在區(qū)間![]() 上恒成立,求
上恒成立,求![]() 的最大值.
的最大值.
【答案】(1)單調(diào)遞減區(qū)間是![]() (2)見解析(3)1
(2)見解析(3)1
【解析】試題分析:(1)第(1)問,直接利用導(dǎo)數(shù)求函數(shù)的減區(qū)間. (2) 利用導(dǎo)數(shù)求函數(shù)的單調(diào)性,從而求出函數(shù)的最大值,需要分類討論. (3)利用第(2)問的結(jié)論,即![]() ,求出a的最大值.
,求出a的最大值.
試題解析:(1)當(dāng)![]() 時,
時,![]() .
. ![]()
令![]() .
.
所以 函數(shù)![]() 的單調(diào)遞減區(qū)間是
的單調(diào)遞減區(qū)間是![]() .
.
(2)![]() .
.
令![]() ,由
,由![]() ,解得
,解得![]() .
.
當(dāng)![]() ,即
,即![]() 時,在區(qū)間
時,在區(qū)間![]() 上
上![]() ,函數(shù)
,函數(shù)![]() 是減函數(shù).
是減函數(shù).
所以 函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值為
上的最大值為![]() ;
;
當(dāng)![]() ,即
,即![]() 時,x在
時,x在![]() 上變化時,
上變化時,![]() 的變化情況如下表
的變化情況如下表
x | 1 |
|
|
|
| 0 | + | 0 | _ |
f(x) |
| 極大值 |
|
所以 函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值為
上的最大值為![]() .
.
綜上所述:當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值為
上的最大值為![]() ;
;
當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值為
上的最大值為![]() .
.
(3)由(Ⅱ)可知:當(dāng)![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 上恒成立;
上恒成立;
當(dāng)![]() 時,由于
時,由于![]() 在區(qū)間
在區(qū)間![]() 上是增函數(shù),
上是增函數(shù),
所以![]() ,即在區(qū)間
,即在區(qū)間![]() 上存在
上存在![]() 使得
使得![]() .
.
綜上所述,a的最大值為1.


 浙大優(yōu)學(xué)小學(xué)年級銜接捷徑浙江大學(xué)出版社系列答案
浙大優(yōu)學(xué)小學(xué)年級銜接捷徑浙江大學(xué)出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,角
,角![]() 的終邊經(jīng)過點
的終邊經(jīng)過點![]() .若
.若![]() 是
是![]() 的圖象上任意兩點,且當(dāng)
的圖象上任意兩點,且當(dāng)![]() 時,
時,![]() 的最小值為
的最小值為![]() .
.
(1)求 ![]() 或
或![]() 的值;
的值;
(2)求函數(shù)![]() 在
在![]() 上的單調(diào)遞減區(qū)間;
上的單調(diào)遞減區(qū)間;
(3)當(dāng)![]() 時,不等式
時,不等式![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,長方體ABCD﹣A1B1C1D1中,點M在棱BB1上,兩條直線MA,MC與平面ABCD所成角均為θ,AC與BD交于點O. 
(1)求證:AC⊥OM;
(2)當(dāng)M為BB1的中點,且θ= ![]() 時,求二面角A﹣D1M﹣B1的余弦值.
時,求二面角A﹣D1M﹣B1的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】正四面體ABCD中,M是棱AD的中點,O是點A在底面BCD內(nèi)的射影,則異面直線BM與AO所成角的余弦值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】[選修4-1:幾何證明選講]
如圖,在正方形ABCD中,E,G分別在邊DA,DC上(不與端點重合),且DE=DG,過D點作DF⊥CE,垂足為F.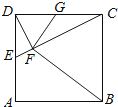
(1)證明:B,C,G,F(xiàn)四點共圓;
(2)若AB=1,E為DA的中點,求四邊形BCGF的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線![]() :
: ![]() 與橢圓
與橢圓![]() :
: ![]() 在第一象限的交點為
在第一象限的交點為![]() ,
, ![]() 為坐標(biāo)原點,
為坐標(biāo)原點, ![]() 為橢圓的右頂點,
為橢圓的右頂點, ![]() 的面積為
的面積為![]() .
.

(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)過![]() 點作直線
點作直線![]() 交
交![]() 于
于![]() 、
、![]() 兩點,射線
兩點,射線![]() 、
、![]() 分別交
分別交![]() 于
于![]() 、
、![]() 兩點,記
兩點,記![]() 和
和![]() 的面積分別為
的面積分別為![]() 和
和![]() ,問是否存在直線
,問是否存在直線![]() ,使得
,使得![]() ?若存在,求出直線
?若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的值域為
上的值域為![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 對任意的
對任意的![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若函數(shù)![]() 有3個零點,求實數(shù)
有3個零點,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某城市城鎮(zhèn)化改革過程中最近五年居民生活水平用水量逐年上升,下表是2011至2015年的統(tǒng)計數(shù)據(jù):
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
居民生活用水量(萬噸) | 236 | 246 | 257 | 276 | 286 |
(1)利用所給數(shù)據(jù)求年居民生活用水量與年份之間的回歸直線方程y=bx+a;
(2)根據(jù)改革方案,預(yù)計在2020年底城鎮(zhèn)化改革結(jié)束,到時候居民的生活用水量將趨于穩(wěn)定,預(yù)計該城市2023年的居民生活用水量.
參考公式:  .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】棱臺![]() 的三視圖與直觀圖如圖所示.
的三視圖與直觀圖如圖所示.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ?若存在,指出點
?若存在,指出點![]() 的位置;若不存在,說明理由.
的位置;若不存在,說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com