Question

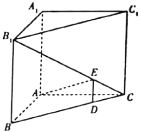
【題目】如圖，在直三棱柱中，，，點D，E分別是線段BC，上的動點（不含端點），且．則下列說法正確的是（ ）

A.平面

B.該三棱柱的外接球的表面積為

C.異面直線與所成角的正切值為

D.二面角的余弦值為

Answer 1

【答案】AD

【解析】

由平行線分線段成比例可知，可判斷A；由題意知直三棱柱是長方體沿對角面切開的一半，故外接球為長方體外接球，球心在中點，即可判斷B；，所以異面直線與所成角為，求解即可判斷C；以A為坐標(biāo)原點，以，，的方向分別為x，y，z軸的正方向建立空間直角坐標(biāo)系，利用向量法求二面角即可判斷D.

在直三棱柱中，四邊形是矩形，

因為，所以，不在平面內(nèi)，平面，

所以平面，A項正確；

因為，所以，

因為，所以，所以，

易知是三棱柱外接球的直徑，

所以三棱柱外接球的表面積為，所以B項錯誤；

因為，所以異面直線與所成角為．

在中，，，

所以，所以C項錯誤；

二面角即二面角，

以A為坐標(biāo)原點，以，，的方向分別為x，y，z軸的正方向建立空間直角坐標(biāo)系，如圖

則，

,,,

設(shè)平面的法向量，

則，即，令可得，

設(shè)平面的一個法向量為，

則，即，令可得

故二面角的余弦值為，所以D項正確．

故選：AD