
制定投資計劃時,不僅要考慮可能獲得的盈利,而且要考慮可能出現的虧損.某投資人打算投資甲、乙兩個項目.根據預測,甲、乙項目可能的最大盈利率分別為100%和50%,可能的最大虧損分別為30%和10%.投資人計劃投資金額不超過10萬元,要求確保可能的資金虧損不超過1.8萬元.問投資人對甲、乙兩個項目各投資多少萬元,才能使可能的盈利最大?
投資甲項目4萬元,乙項目6萬元.
解析試題分析:(1)含有實際背景的線性規劃問題其解題關鍵是找到制約求解目標的兩個變量,用這兩個變量建立可行域和目標函數,解題時要注意題目中的各種制約的關系,列出全面的制約條件和正確的目標函數;(2)平面區域的畫法:線定界、點定線(注意實虛線);(3)求最值:求二元一次函數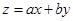 的最值,將函數
的最值,將函數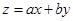 轉化為直線的點斜式
轉化為直線的點斜式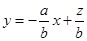 ,通過求直線的截距
,通過求直線的截距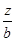 的最值間接求出
的最值間接求出 的最值,最優解在頂點或邊界取得.
的最值,最優解在頂點或邊界取得.
試題解析:解:設分別向甲、乙兩組項目投資 萬元,
萬元, 萬元,利潤為
萬元,利潤為 萬元
萬元
由題意知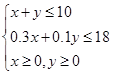
目標函數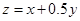 作出可行域
作出可行域
作出可行域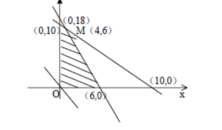
作直線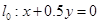 ,并作平行直線
,并作平行直線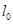 的一組直線
的一組直線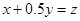
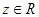 ,與可行域相交,其中有一條直線經過可行域上的點
,與可行域相交,其中有一條直線經過可行域上的點 點,且與直線
點,且與直線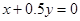 的距離
的距離
最大,這里 是直線
是直線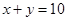 和
和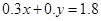
解方程組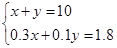 ,解得
,解得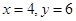
此時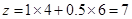 (萬元)
(萬元)
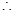 當
當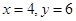 時
時 最大
最大
答:投資人投資甲項目4萬元,乙項目6萬元,獲得利潤最大
考點:利用線性規劃求目標函數的最值.


科目:高中數學 來源: 題型:解答題
已知二次函數f(x)滿足:①當x=1時有極值;②圖象與y軸交點的縱坐標為﹣3,且在該點處的切線與直線x=2y﹣4垂直.
(1)求f(1)的值;
(2)若函數g(x)=f(lnx),x∈(1,+∞)上任意一點處的切線斜率恒大于a2﹣a﹣2,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某房地產開發公司計劃在一樓區內建造一個長方形公園ABCD,公園由長方形休閑區A1B1C1D1和環公園人行道(陰影部分)組成.已知休閑區A1B1C1D1的面積為4000m2,人行道的寬分別為4m和10m(如圖所示).
(1)若設休閑區的長和寬的比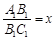 ,求公園ABCD所占面積S關于x的函數解析式;
,求公園ABCD所占面積S關于x的函數解析式;
(2)要使公園所占面積最小,休閑區A1B1C1D1的長和寬應如何設計?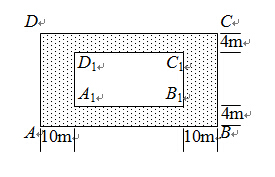
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com