
【題目】某企業生產一種產品,從流水線上隨機抽取100件產品,統計其質量指標值并繪制頻率分布直方圖(如圖):
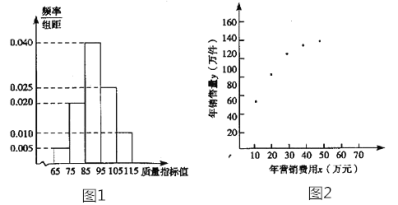
規定產品的質量指標值在![]() 的為劣質品,在
的為劣質品,在![]() 的為優等品,在
的為優等品,在![]() 的為特優品,銷售時劣質品每件虧損1元,優等品每件盈利3元,特優品每件盈利5元.以這100 件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
的為特優品,銷售時劣質品每件虧損1元,優等品每件盈利3元,特優品每件盈利5元.以這100 件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
(1)求每件產品的平均銷售利潤;
(2)該企業為了解年營銷費用![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:萬件)的影響,對近5年年營銷費用
(單位:萬件)的影響,對近5年年營銷費用![]() 和年銷售量
和年銷售量![]() 數據做了初步處理,得到如圖的散點圖及一些統計量的值.
數據做了初步處理,得到如圖的散點圖及一些統計量的值.
|
|
|
|
16.30 | 23.20 | 0.81 | 1.62 |
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根據散點圖判斷,![]() 可以作為年銷售量
可以作為年銷售量![]() (萬件)關于年營銷費用
(萬件)關于年營銷費用![]() (萬元)的回歸方程.
(萬元)的回歸方程.
①求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
⑦用所求的回歸方程估計該企業應投人多少年營銷費,才能使得該企業的年收益的預報值達到最大?(收益=銷售利潤營銷費用,取![]() )
)
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() 其回歸直線
其回歸直線![]() 均斜率和截距的最小二乘估計分別為
均斜率和截距的最小二乘估計分別為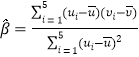 ,
,![]() .
.
【答案】(1)3;(2)①![]() ,②900萬元.
,②900萬元.
【解析】
(1)先設每件產品的銷售利潤為![]() ,判斷出
,判斷出![]() 的可能取值,根據頻率分布直方圖求出對應概率,進而得出分布列,求出期望;
的可能取值,根據頻率分布直方圖求出對應概率,進而得出分布列,求出期望;
(2)①先由![]() 得,
得,![]() ,令
,令![]() ,
,![]() ,
,![]() ,則
,則![]() ,根據表中數據求出
,根據表中數據求出![]() ,
,![]() ,進而可得
,進而可得![]() ,從而可得
,從而可得![]() ,整理即可求出結果;
,整理即可求出結果;
②設年收益為![]() 萬元,則
萬元,則![]() ,令
,令![]() ,則
,則![]() ,進而可求出結果.
,進而可求出結果.
(1)設每件產品的銷售利潤為![]() ,則
,則![]() 的可能取值為-1,3,5由頻率分布直方圖可得產品為劣質品、優等品、特優品的概率分別為0.05,0.85,0.1.所以
的可能取值為-1,3,5由頻率分布直方圖可得產品為劣質品、優等品、特優品的概率分別為0.05,0.85,0.1.所以![]() ;
;![]() ;
;![]() ,…
,…
所以![]() 的分布列為
的分布列為
| -1 | 3 | 5 |
| 0.05 | 0.85 | 0.1 |
所以![]() (元).
(元).
即每件產品的平均銷售利潤為3元.
(2)①由![]() 得,
得,![]() .
.
令![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,
由表中數據可得,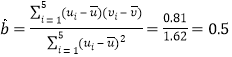 ,
,
則![]() .
.
所以![]() ,即
,即![]() .
.
因為![]() ,所以
,所以![]() ,故所求的回歸方程為
,故所求的回歸方程為![]() .
.
②設年收益為![]() 萬元,則
萬元,則![]() .
.
令![]() ,則
,則![]() ,
,
所以當![]() ,即
,即![]() 時,
時,![]() 有最大值900.
有最大值900.
即該企業應該投入900萬元營銷費,能使得該企業的年收益的預報值達到最大900萬元.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】微信是騰訊公司推出的一種手機通訊軟件,它支持發送語音短信、視頻、圖片和文字,一經推出便風靡全國,甚至涌現出一批在微信的朋友圈內銷售商品的人(被稱為微商).為了調查每天微信用戶使用微信的時間,某經銷化妝品的微商在一廣場隨機采訪男性、女性用戶各![]() 名,將男性、女性使用微信的時間分成
名,將男性、女性使用微信的時間分成![]() 組:
組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別加以統計,得到如圖所示的頻率分布直方圖.
分別加以統計,得到如圖所示的頻率分布直方圖.

(1)根據女性頻率分布直方圖,估計女性使用微信的平均時間;
(2)若每天玩微信超過![]() 小時的用戶列為“微信控”,否則稱其為“非微信控”,請你根據已知條件完成
小時的用戶列為“微信控”,否則稱其為“非微信控”,請你根據已知條件完成![]() 的列聯表,并判斷是否有
的列聯表,并判斷是否有![]() 的把握認為“微信控”與“性別”有關?
的把握認為“微信控”與“性別”有關?
參考公式:![]() ,其中
,其中![]() .
.
參考數據:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點與短軸的一個端點是等邊三角形的三個頂點,且長軸長為4
的兩個焦點與短軸的一個端點是等邊三角形的三個頂點,且長軸長為4
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 是橢圓
是橢圓![]() 的左頂點,經過左焦點
的左頂點,經過左焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,求
兩點,求![]() 與
與![]() 的面積之差的絕對值的最大值,并求取得最大值時直線
的面積之差的絕對值的最大值,并求取得最大值時直線![]() 的方程.
的方程.![]() 為坐標原點)
為坐標原點)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的右焦點為
的右焦點為![]() ,右頂點為
,右頂點為![]() .已知
.已知![]() ,其中
,其中![]() 為原點,
為原點, ![]() 為橢圓的離心率.
為橢圓的離心率.
(1)求橢圓的方程及離心率![]() 的值;
的值;
(2)設過點![]() 的直線
的直線![]() 與橢圓交于點
與橢圓交于點![]() (
(![]() 不在
不在![]() 軸上),垂直于
軸上),垂直于![]() 的直線與
的直線與![]() 交于點
交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .若
.若![]() ,且
,且![]() ,求直線
,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設常數![]() .在平面直角坐標系xOy中,已知點
.在平面直角坐標系xOy中,已知點![]() ,直線l:
,直線l:![]() ,曲線Γ:
,曲線Γ:![]() (
(![]() ,
,![]() ).l與x軸交于點A、與Γ交于點B.P、Q分別是曲線Γ與線段AB上的動點.
).l與x軸交于點A、與Γ交于點B.P、Q分別是曲線Γ與線段AB上的動點.
(1)用t表示點B到點F的距離;
(2)設![]() ,
,![]() ,線段OQ的中點在直線FP上,求△AQP的面積;
,線段OQ的中點在直線FP上,求△AQP的面積;
(3)設![]() ,是否存在以FP、FQ為鄰邊的矩形FPEQ,使得點E在Γ上?若存在,求點P的坐標;若不存在,說明理由.
,是否存在以FP、FQ為鄰邊的矩形FPEQ,使得點E在Γ上?若存在,求點P的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() (
(![]() 為參數).以原點
為參數).以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 與直線
與直線![]() 交于
交于![]() 兩點,點
兩點,點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 經過點
經過點![]() 離心率
離心率![]() .
.
(Ⅰ)求橢圓的方程;
(Ⅱ)經過橢圓左焦點![]() 的直線(不經過點
的直線(不經過點![]() 且不與
且不與![]() 軸重合)與橢圓交于
軸重合)與橢圓交于![]() 兩點,與直線
兩點,與直線![]() :
:![]() 交于點
交于點![]() ,記直線
,記直線![]() 的斜率分別為
的斜率分別為![]() .則是否存在常數
.則是否存在常數![]() ,使得向量
,使得向量![]()
![]() 共線?若存在求出
共線?若存在求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,底面ABCD是邊長為3的正方形,EFG分別是棱ABPBPC的中點,
,底面ABCD是邊長為3的正方形,EFG分別是棱ABPBPC的中點,![]() ,
,![]() .
.

(Ⅰ)求證:平面EFG∥平面PAD;
(Ⅱ)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等腰直角三角形![]() 中,
中,![]() ,點
,點![]() 在邊
在邊![]() 上,
上,![]() 垂直
垂直![]() 交
交![]() 于
于![]() ,如圖①.將
,如圖①.將![]() 沿
沿![]() 折起,使
折起,使![]() 到達
到達![]() 的位置,且使平面
的位置,且使平面![]() 平面
平面![]() ,連接
,連接![]() ,
,![]() ,如圖②.
,如圖②.
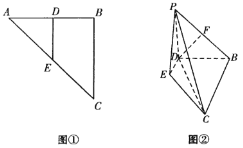
(Ⅰ)若![]() 為
為![]() 的中點,
的中點,![]() ,求證:
,求證:![]() ;
;
(Ⅱ)若![]() ,當三棱錐
,當三棱錐![]() 的體積最大時,求二面角
的體積最大時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com