
【題目】已知點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,動圓
,動圓![]() 與
與![]() 軸相切于點(diǎn)
軸相切于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 的直線
的直線![]() 與圓
與圓![]() 相切于點(diǎn)
相切于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 的直線
的直線![]() 與圓
與圓![]() 相切于點(diǎn)
相切于點(diǎn)![]() (
(![]() 均不同于點(diǎn)
均不同于點(diǎn)![]() ),且
),且![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,設(shè)點(diǎn)
,設(shè)點(diǎn)![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)證明:![]() 為定值,并求
為定值,并求![]() 的方程;
的方程;
(2)設(shè)直線![]() 與
與![]() 的另一個交點(diǎn)為
的另一個交點(diǎn)為![]() ,直線
,直線![]() 與
與![]() 交于
交于![]() 兩點(diǎn),當(dāng)
兩點(diǎn),當(dāng)![]() 三點(diǎn)共線時,求四邊形
三點(diǎn)共線時,求四邊形![]() 的面積.
的面積.
【答案】(1)證明見解析,方程為![]() .
.
(2) ![]() .
.
【解析】分析:(1)根據(jù)圓的切線性質(zhì)可得,![]()
![]() ,從而根據(jù)橢圓的可得結(jié)果;(2)直線與曲線聯(lián)立,利用韋達(dá)定理、弦長公式以及三角形面積公式可得四邊形
,從而根據(jù)橢圓的可得結(jié)果;(2)直線與曲線聯(lián)立,利用韋達(dá)定理、弦長公式以及三角形面積公式可得四邊形![]() 的面積為
的面積為![]() .
.
詳解:(1)由已知可得|PD|=|PE|,|BA|=|BD|,|CE|=|CA|,
所以|PB|+|PC|=|PD|+|DB|+|PC|
=|PE|+|PC|+|AB|
=|CE|+|AB|
=|AC|+|AB|=4>|BC|
所以點(diǎn)P的軌跡是以B,C為焦點(diǎn)的橢圓(去掉與x軸的交點(diǎn)),
可求的方程為![]() +
+![]() =1(y≠0).
=1(y≠0).
(2)由O,D,C三點(diǎn)共線及圓的幾何性質(zhì),可知PB⊥CD,
又由直線CE,CA為圓O的切線,可知CE=CA,OA=OE,
所以△OAC≌△OEC,進(jìn)而有∠ACO=∠ECO,
所以|PC|=|BC|=2,又由橢圓的定義,|PB|+|PC|=4,得|PB|=2,
所以△PBC為等邊三角形,即點(diǎn)P在y軸上,點(diǎn)P的坐標(biāo)為(0,±![]() )
)
(i)當(dāng)點(diǎn)P的坐標(biāo)為(0,![]() )時,∠PBC=60,∠BCD=30,
)時,∠PBC=60,∠BCD=30,
此時直線l1的方程為y=![]() (x+1),直線CD的方程為y=-
(x+1),直線CD的方程為y=-![]() (x-1),
(x-1),
由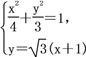 整理得5x2+8x=0,得Q(-
整理得5x2+8x=0,得Q(-![]() ,-
,-![]() ),所以|PQ|=
),所以|PQ|=![]() ,
,
由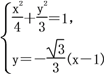 整理得13x2-8x-32=0,
整理得13x2-8x-32=0,
設(shè)M(x1,y1),N(x2,y2),x1+x2=![]() ,x1x2=-
,x1x2=-![]() ,
,
|MN|=![]() |x1-x2|=
|x1-x2|=![]() ,
,
所以四邊形MPNQ的面積S=![]() |PQ|·|MN|=
|PQ|·|MN|=![]() .
.
(ii)當(dāng)點(diǎn)P的坐標(biāo)為(0,-![]() )時,由橢圓的對稱性,四邊形MPNQ的面積為
)時,由橢圓的對稱性,四邊形MPNQ的面積為![]() .
.
綜上,四邊形MPNQ的面積為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的是( )
A. 甲、乙二人比賽,甲勝的概率為![]() ,則比賽5場,甲勝3場
,則比賽5場,甲勝3場
B. 某醫(yī)院治療一種疾病的治愈率為10%,前9個病人沒有治愈,則第10個病人一定治愈
C. 隨機(jī)試驗的頻率與概率相等
D. 天氣預(yù)報中,預(yù)報明天降水概率為90%,是指降水的可能性是90%
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的一個焦點(diǎn)為
的一個焦點(diǎn)為![]() ,且離心率為
,且離心率為![]() .
.
(1)求橢圓方程;
(2)斜率為![]() 的直線
的直線![]() 過點(diǎn)F,且與橢圓交于
過點(diǎn)F,且與橢圓交于![]() 兩點(diǎn),P為直線
兩點(diǎn),P為直線![]() 上的一點(diǎn),
上的一點(diǎn),
若![]() 為等邊三角形,求直線
為等邊三角形,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,AD⊥平面PAB,AP⊥AB.

(1)求證:CD⊥AP;
(2)若CD⊥PD,求證:CD∥平面PAB;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左焦點(diǎn)
的左焦點(diǎn)![]() ,離心率為
,離心率為![]() ,點(diǎn)
,點(diǎn)![]() 為橢圓
為橢圓![]() 上任一點(diǎn),且
上任一點(diǎn),且![]() 的最小值為
的最小值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 過橢圓的左焦點(diǎn)
過橢圓的左焦點(diǎn)![]() ,與橢圓交于
,與橢圓交于![]() 兩點(diǎn),且
兩點(diǎn),且![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
![]()
(1)若函數(shù)![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 平行,求實數(shù)
平行,求實數(shù)![]() 的值;
的值;
(2)試討論函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上最大值;
上最大值;
(3)若![]() 時,函數(shù)
時,函數(shù)![]() 恰有兩個零點(diǎn)
恰有兩個零點(diǎn)![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一個正方體的平面展開圖及該正方體的直觀圖的示意圖如圖所示.
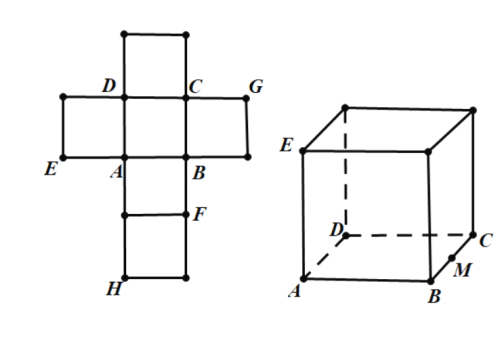
(Ⅰ)請按字母F,G,H標(biāo)記在正方體相應(yīng)地頂點(diǎn)處(不需要說明理由)
(Ⅱ)判斷平面BEG與平面ACH的位置關(guān)系.并說明你的結(jié)論.
(Ⅲ)證明:直線DF![]() 平面BEG
平面BEG
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列四種說法正確的是( )
①若![]() 和
和![]() 都是定義在
都是定義在![]() 上的函數(shù),則“
上的函數(shù),則“![]() 與
與![]() 同是奇函數(shù)”是“
同是奇函數(shù)”是“![]() 是偶函數(shù)”的充要條件
是偶函數(shù)”的充要條件
②命題 “![]() ”的否定是“
”的否定是“![]()
![]() ≤0”
≤0”
③命題“若x=2,則![]() ”的逆命題是“若
”的逆命題是“若![]() ,則x=2”
,則x=2”
④命題![]() :在
:在![]() 中,若
中,若![]() ,則
,則![]() ;
;
命題![]() :
:![]() 在第一象限是增函數(shù);
在第一象限是增函數(shù);
則![]() 為真命題
為真命題
A. ①②③④ B. ①③ C. ③④ D. ③
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
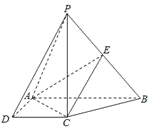
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點(diǎn).
的中點(diǎn).
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值為
的余弦值為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com