
【題目】設a>0,b>0( )
A.若lna+2a=lnb+3b,則a>b
B.2a+2a=2b+3b,則a<b
C.若lna﹣2a=lnb﹣3b,則a>b
D.2a﹣2a=2b﹣3b,則a<b
【答案】A
【解析】解:∵lna+2a=lnb+3b,
∴a>0,b>0,
∴lna+2a=lnb+2b+b,
∴lna+2a>lnb+2b,
∵y=lnx+2x是增函數,
∴a>b.所以A正確;
同理B錯誤;
lna﹣2a=lnb﹣3b,
∴a>0,b>0,
∴lna﹣2a=lnb﹣2b﹣b,
∴lna﹣2a<lnb﹣2b,構造函數f(x)=lnx﹣2x,
則f′(x)= ![]() ﹣2<0,
﹣2<0,
故f(x)在(1,+∞)單調遞減,
∴a>b,0<x<1時,
y=lnx﹣2x是增函數,
∴a<b.所以C不正確;
同理D不正確.
故選:A.
【考點精析】本題主要考查了命題的真假判斷與應用和對數的運算性質的相關知識點,需要掌握兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關系;①加法:![]() ②減法:
②減法:![]() ③數乘:
③數乘:![]() ④
④![]() ⑤
⑤![]() 才能正確解答此題.
才能正確解答此題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖ABCD是平面四邊形,∠ADB=∠BCD=90°,AB=4,BD=2.
(Ⅰ)若BC=1,求AC的長;
(Ⅱ)若∠ACD=30°,求tan∠BDC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四面體ABCD中,AB、BC、BD兩兩垂直,AB=BC=BD=4,E、F分別為棱BC、AD的中點. 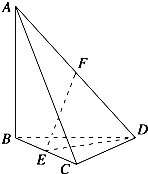
(1)求異面直線AB與EF所成角的余弦值;
(2)求E到平面ACD的距離;
(3)求EF與平面ACD所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知(1+3x)n的展開式中,末三項的二項式系數的和等于121,求:
(1) 展開式中二項式系數最大的項;
(2) 展開式中系數最大的項.(結果可以以組合數形式表示)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某競賽的題庫系統有60%的自然科學類題目,40%的文化生活類題目(假設題庫中的題目總數非常大),參賽者需從題庫中抽取3個題目作答,有兩種抽取方法:方法一是直接從題庫中隨機抽取3個題目;方法二是先在題庫中按照題目類型用分層抽樣的方法抽取10個題目作為樣本,再從這10個題目中任意抽取3個題目.
(1)兩種方法抽取的3個題目中,恰好有1個自然科學類題目和2個文化生活類題目的概率是否相同?若相同,說明理由;若不同,分別計算出兩種抽取方法對應的概率.
(2)已知某參賽者抽取的3個題目恰好有1個自然科學類題目和2個文化生活類題目,且該參賽者答對自然科學類題目的概率為![]() ,答對文化生活類題目的概率為
,答對文化生活類題目的概率為![]() .設該參賽者答對的題目數為X,求X的分布列和數學期望.
.設該參賽者答對的題目數為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等比數列{an}中,a2=3,a5=81,bn=1+2log3an .
(1)求數列{bn}的前n項的和;
(2)已知數列 ![]() 的前項的和為Sn , 證明:
的前項的和為Sn , 證明: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經過對K2的統計量的研究,得到了若干個觀測值,當K2≈6.706時,我們認為兩分類變量A、B( )
A. 有67.06%的把握認為A與B有關系 B. 有99%的把握認為A與B有關系
C. 有0.010的把握認為A與B有關系 D. 沒有充分理由說明A與B有關系
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為提升學生的英語學習能力,進行了主題分別為“聽”、“說”、“讀”、“寫”四場競賽.規定:每場競賽的前三名得分分別為![]() ,
,![]() ,
,![]() (
(![]() ,且
,且![]() ,
,![]() ,
,![]() ),選手的最終得分為各場得分之和.最終甲、乙、丙三人包攬了每場競賽的前三名,在四場競賽中,已知甲最終分為
),選手的最終得分為各場得分之和.最終甲、乙、丙三人包攬了每場競賽的前三名,在四場競賽中,已知甲最終分為![]() 分,乙最終得分為
分,乙最終得分為![]() 分,丙最終得分為
分,丙最終得分為![]() 分,且乙在“聽”這場競賽中獲得了第一名,則“聽”這場競賽的第三名是( )
分,且乙在“聽”這場競賽中獲得了第一名,則“聽”這場競賽的第三名是( )
A. 甲 B. 乙 C. 丙 D. 甲和丙都有可能
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=cos ![]() ,g(x)=exf(x),其中e為自然對數的底數.
,g(x)=exf(x),其中e為自然對數的底數.
(1)求曲線y=g(x)在點(0,g(0))處的切線方程;
(2)若對任意 ![]() 時,方程g(x)=xf(x)的解的個數,并說明理由.
時,方程g(x)=xf(x)的解的個數,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com