
【題目】已知函數(shù)f(x)=x3+bx2+cx的極值點(diǎn)為x=﹣ ![]() 和x=1
和x=1
(1)求b,c的值與f(x)的單調(diào)區(qū)間
(2)當(dāng)x∈[﹣1,2]時,不等式f(x)<m恒成立,求實(shí)數(shù)m的取值范圍.
【答案】
(1)解:∵f(x)=x3+bx2+cx,
∴f'(x)=3x2+2bx+c,
∵f(x)的極值點(diǎn)為x=﹣ ![]() 和x=1
和x=1
∴f'(1)=3+2b+c=0,f'(- ![]() )=
)= ![]() ﹣
﹣ ![]() b+c=0,
b+c=0,
解得,b= ![]() ,c=﹣2,
,c=﹣2,
∴f'(x)=(3x+2)(x﹣1),
當(dāng)f'(x)>0時,解得x<﹣ ![]() ,或x>1,
,或x>1,
當(dāng)f'(x)<0時,解得﹣ ![]() <x<1,
<x<1,
故函數(shù)f(x)的單調(diào)遞增區(qū)間為(﹣∞,﹣ ![]() )和(1,+∞),單調(diào)減區(qū)間為(﹣
)和(1,+∞),單調(diào)減區(qū)間為(﹣ ![]() ,1)
,1)
(2)解:有(1)知f(x)=x3﹣ ![]() x2﹣2x,x∈[﹣1,2],
x2﹣2x,x∈[﹣1,2],
故函數(shù)在[﹣1,﹣ ![]() )和(1,2]單調(diào)遞增增,在(﹣
)和(1,2]單調(diào)遞增增,在(﹣ ![]() ,1)單調(diào)遞減,
,1)單調(diào)遞減,
當(dāng)x=﹣ ![]() ,函數(shù)有極大值,f(-
,函數(shù)有極大值,f(- ![]() )=
)= ![]() ,f(2)=2,
,f(2)=2,
所以函數(shù)的最大值為2,
所以不等式f(x)<m在x∈[﹣1,2]時恒成立,
故m>2
故實(shí)數(shù)m的取值范圍為(2,+∞)
【解析】(1)對函數(shù)進(jìn)行求導(dǎo),令f'(1)=0,f'(- ![]() )=0可求出b,c的值,再利用導(dǎo)數(shù)求出函數(shù)單調(diào)區(qū)間即可.(2)根據(jù)函數(shù)的單調(diào)性求出f(x)在[﹣1,2]上的最大值,繼而求出m的范圍
)=0可求出b,c的值,再利用導(dǎo)數(shù)求出函數(shù)單調(diào)區(qū)間即可.(2)根據(jù)函數(shù)的單調(diào)性求出f(x)在[﹣1,2]上的最大值,繼而求出m的范圍
【考點(diǎn)精析】通過靈活運(yùn)用利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性和函數(shù)的極值與導(dǎo)數(shù),掌握一般的,函數(shù)的單調(diào)性與其導(dǎo)數(shù)的正負(fù)有如下關(guān)系: 在某個區(qū)間![]() 內(nèi),(1)如果
內(nèi),(1)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調(diào)遞增;(2)如果
在這個區(qū)間單調(diào)遞增;(2)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調(diào)遞減;求函數(shù)
在這個區(qū)間單調(diào)遞減;求函數(shù)![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側(cè)
附近的左側(cè)![]() ,右側(cè)
,右側(cè)![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側(cè)
附近的左側(cè)![]() ,右側(cè)
,右側(cè)![]() ,那么
,那么![]() 是極小值即可以解答此題.
是極小值即可以解答此題.


 陽光課堂課時優(yōu)化作業(yè)系列答案
陽光課堂課時優(yōu)化作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,直線
,直線![]() 為曲線
為曲線![]() 的切線(
的切線(![]() 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
(1)求實(shí)數(shù)![]() 的值;
的值;
(2)用![]() 表示
表示![]() 中的最小值,設(shè)函數(shù)
中的最小值,設(shè)函數(shù)![]() ,若函數(shù)
,若函數(shù)
![]() 為增函數(shù),求實(shí)數(shù)
為增函數(shù),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若關(guān)于![]() 的方程
的方程![]() 有實(shí)數(shù)根,求實(shí)數(shù)
有實(shí)數(shù)根,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù),![]() 其中
其中![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(Ⅰ)討論函數(shù)![]() 的單調(diào)性及極值;
的單調(diào)性及極值;
(Ⅱ)若不等式![]() 在
在![]() 內(nèi)恒成立,求證:
內(nèi)恒成立,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD的底面為菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
. 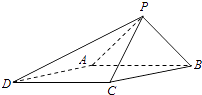
(1)求證:AB⊥PC;
(2)求二面角B一PC﹣D的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)=sin( ![]() ﹣
﹣ ![]() )﹣2cos2
)﹣2cos2 ![]() +1. (Ⅰ)求f(x)的最小正周期;
+1. (Ⅰ)求f(x)的最小正周期;
(Ⅱ)若函數(shù)y=g(x)與y=f(x)的圖象關(guān)于直線x=1對稱,求當(dāng)x∈[0, ![]() ]時y=g(x)的最大值.
]時y=g(x)的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】等比數(shù)列{an}的各項(xiàng)均為正數(shù),且2a1+3a2=1,a32=9a2a6 , (Ⅰ)求數(shù)列{an}的通項(xiàng)公式;
(Ⅱ)設(shè)bn=log3a1+log3a2+…+log3an , 求數(shù)列{ ![]() }的前n項(xiàng)和.
}的前n項(xiàng)和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】袋中有形狀和大小完全相同的四種不同顏色的小球,每種顏色的小球各有4個,分別編號為1,2,3,4.現(xiàn)從袋中隨機(jī)取兩個球.
(Ⅰ)若兩個球顏色不同,求不同取法的種數(shù);
(Ⅱ)在(1)的條件下,記兩球編號的差的絕對值為隨機(jī)變量X,求隨機(jī)變量X的概率分布與數(shù)學(xué)期望.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com