
���}Ŀ����D��![]() �LjAO��ֱ�����c(di��n)C�LjAO�Ϯ���A��B���c(di��n)��ֱ��
�LjAO��ֱ�����c(di��n)C�LjAO�Ϯ���A��B���c(di��n)��ֱ��![]() ƽ��
ƽ��![]() ��E��F�քe��
��E��F�քe��![]() ��
��![]() �����c(di��n).
�����c(di��n).

��1��ӛƽ��![]() �cƽ��
�cƽ��![]() �Ľ�����l��ԇ�Д�ֱ��l�cƽ��
�Ľ�����l��ԇ�Д�ֱ��l�cƽ��![]() ��λ���P(gu��n)ϵ���������C����
��λ���P(gu��n)ϵ���������C����
��2���O(sh��)![]() ��������
��������![]() ��С��ȡֵ����.
��С��ȡֵ����.
���𰸡���1��ƽ�У�ԔҊ��������2��![]() .
.
��������
��1�����C![]() ƽ��
ƽ��![]() �����C
�����C![]() �����ó�l
�����ó�l![]() ƽ��
ƽ��![]() ��
��
��2���O(sh��)ֱ��l�c�AO����һ�����c(di��n)��D���B��DE��FB����![]() ��
��![]() ���ɵ�
���ɵ�![]() �Ƕ���ǵ�ƽ��ǣ�����
�Ƕ���ǵ�ƽ��ǣ�����![]() �ķ����ó�����ǵ�ȡֵ����.
�ķ����ó�����ǵ�ȡֵ����.
��1��![]()
![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]()
![]() ƽ��
ƽ��![]() ��
��
��![]() ƽ��
ƽ��![]() ��ƽ��
��ƽ��![]() �cƽ��
�cƽ��![]() �Ľ�����l������
�Ľ�����l������![]() ��
��
��l![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ������l
������l![]() ƽ��
ƽ��![]() ��
��
��2���O(sh��)ֱ��l�c�AO����һ�����c(di��n)��D���B��DE��FB����D��
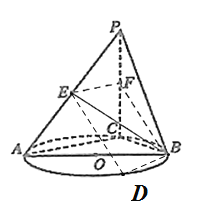
�ɣ�1��֪��BD![]() AC����
AC����![]() ������
������![]() ��
��
����![]() ƽ��
ƽ��![]() ������
������![]() ��
��
��![]() ������
������![]() ƽ��PBC��
ƽ��PBC��
��FB![]() ƽ��PBC������
ƽ��PBC������![]() ��
��
����![]() ���Ƕ����
���Ƕ����![]() ��ƽ��ǣ�
��ƽ��ǣ�
��?y��n)?/span>![]() ���c(di��n)F��
���c(di��n)F��![]() �����c(di��n)������
�����c(di��n)������![]() ��
��
��![]() ��
��
ע�![]() ������
������![]() ������
������![]() ��
��
��?y��n)?/span>![]() ������
������![]() ��
��
���Զ����![]() ��С��ȡֵ������
��С��ȡֵ������![]() .
.


 �ľ��D���n�r���hϵ�д�
�ľ��D���n�r���hϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���ڱ���ij�fС�^(q��)���칤���У���Ҫ�ڵ�����O(sh��)��ȼ?x��)�ܵ?��֪С�^(q��)ij̎�������ݷքeλ������![]() ��������c(di��n)�ϣ��c(di��n)
��������c(di��n)�ϣ��c(di��n)![]() �ǻ�
�ǻ�![]() �����c(di��n)���F(xi��n)���ھ���
�����c(di��n)���F(xi��n)���ھ���![]() ����һ̎�_�ڹ�����
����һ̎�_�ڹ�����![]() �����c�c(di��n)
�����c�c(di��n)![]() ��
��![]() �غϣ�������O(sh��)���l������ȼ?x��)�ܾ�
�غϣ�������O(sh��)���l������ȼ?x��)�ܾ�![]() ��
��![]() ��
��![]() ����֪
����֪![]() �ף�
�ף�![]() ��ӛ
��ӛ![]() ��ԓ���l������ȼ?x��)�ܾ��Ŀ��L�Ȟ�
��ԓ���l������ȼ?x��)�ܾ��Ŀ��L�Ȟ�![]() ��.
��.

��1����![]() ��ʾ��
��ʾ��![]() �ĺ���(sh��)��������
�ĺ���(sh��)��������![]() �ķ�����
�ķ�����
��2��Ո�_��������![]() ��λ�ã�ʹ��̎������ȼ?x��)�ܾ��Ŀ��L����С����������L�ȵ���Сֵ.
��λ�ã�ʹ��̎������ȼ?x��)�ܾ��Ŀ��L����С����������L�ȵ���Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����Ї��Q��ȫ�潨��С��������P(gu��n)�I֮�꣬��θ��õر��Ϻ�������������Ќ�(sh��)����(qi��ng)���ߡ��@�øС����ɞ�![]() ��ȫ���ɕ�����Ҫ�P(gu��n)�У�ij�^(q��)����������{(di��o)���˼ס��ҡ�����������
��ȫ���ɕ�����Ҫ�P(gu��n)�У�ij�^(q��)����������{(di��o)���˼ס��ҡ�����������![]() �������(xi��ng)Ŀ���õ�������Ϣ������ԓ�^(q��)���M(j��n)���(xi��ng)Ŀ���ͱ�����M(j��n)�c֮�������(xi��ng)Ŀ���ڶ�����ɂ��(xi��ng)Ŀ�c�����������P(gu��n)���@�ɂ��(xi��ng)Ŀ����Ҫ���M(j��n)һ�������ҡ����ɂ��(xi��ng)Ŀ֮�g�Л_ͻ���ɂ��(xi��ng)Ŀֻ�����M(j��n)һ�����ܱ������ɂ��(xi��ng)Ŀ�P(gu��n)(li��n)���^�ߣ�Ҫôͬ�r���M(j��n)��Ҫô�������M(j��n)���������M(j��n)�(xi��ng)Ŀ�죬�ס����ɂ��(xi��ng)ĿҲ������M(j��n)���tԓ�^(q��)��(y��ng)���M(j��n)���(xi��ng)Ŀ��( )
�������(xi��ng)Ŀ���õ�������Ϣ������ԓ�^(q��)���M(j��n)���(xi��ng)Ŀ���ͱ�����M(j��n)�c֮�������(xi��ng)Ŀ���ڶ�����ɂ��(xi��ng)Ŀ�c�����������P(gu��n)���@�ɂ��(xi��ng)Ŀ����Ҫ���M(j��n)һ�������ҡ����ɂ��(xi��ng)Ŀ֮�g�Л_ͻ���ɂ��(xi��ng)Ŀֻ�����M(j��n)һ�����ܱ������ɂ��(xi��ng)Ŀ�P(gu��n)(li��n)���^�ߣ�Ҫôͬ�r���M(j��n)��Ҫô�������M(j��n)���������M(j��n)�(xi��ng)Ŀ�죬�ס����ɂ��(xi��ng)ĿҲ������M(j��n)���tԓ�^(q��)��(y��ng)���M(j��n)���(xi��ng)Ŀ��( )
A. �ס���B. ������C. �ҡ���D. �ס���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ڹ̶������������鳣��(sh��)���£���(d��ng)���wͨ�^�A�ιܵ��r�����������ʣ�����λ��![]() ���c�ܵ��돽r����λ��cm�����Ĵη�������.
���c�ܵ��돽r����λ��cm�����Ĵη�������.
��1���������w�������ʣ��P(gu��n)�ڹܵ��돽r�ĺ���(sh��)����ʽ��
��2�������w�ڰ돽��3cm�Ĺܵ��У��������ʞ�![]() ����ԓ���wͨ�^�돽��r�Ĺܵ��r������������v�ı��_(d��)ʽ��
����ԓ���wͨ�^�돽��r�Ĺܵ��r������������v�ı��_(d��)ʽ��
��3����֪��2���еĚ��wͨ�^�Ĺܵ��돽��5cm��Ӌ(j��)��ԓ���w���������ʣ����_��![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���D��1����ij�l������܇��·��֧���~y�P(gu��n)�ڳ˿���x�ĈD��.



��1��ԇ�f���D��1�����c(di��n)A���c(di��n)B�Լ��侀AB�ϵ��c(di��n)�Č�(sh��)�H���x��
��2������Ŀǰ���l��·̝�p����˾���P(gu��n)�ˆT����˃ɷNŤ̝���A�Ľ��h����D��2����3����ʾ�����ܸ���(j��)�D���f���@�ɷN���h��ʲô�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���}![]() ���P(gu��n)��
���P(gu��n)��![]() �IJ���ʽ
�IJ���ʽ![]() �o�⣻���}
�o�⣻���}![]() ��ָ��(sh��)����(sh��)
��ָ��(sh��)����(sh��)![]() ��
��![]() �ϵ�������(sh��).
�ϵ�������(sh��).
��1�������}![]() �������}����(sh��)��(sh��)
�������}����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��2�����M��![]() ������}��
������}��![]() �������}��(sh��)��(sh��)
�������}�Č�(sh��)��(sh��)![]() ȡֵ�����Ǽ���
ȡֵ�����Ǽ���![]() ������
������![]() ����
����![]() ����(sh��)��(sh��)
����(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]()
![]() ���x���ʞ�
���x���ʞ�![]() ����ԭ�c(di��n)��A�ģ��E�A�Ķ̰��S��돽�ĈA�cֱ��
����ԭ�c(di��n)��A�ģ��E�A�Ķ̰��S��돽�ĈA�cֱ��![]() ���У��^�c(di��n)
���У��^�c(di��n)![]() �Ҳ���ֱ��
�Ҳ���ֱ��![]() �Sֱ��
�Sֱ��![]() �c�E�A
�c�E�A![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)��
���c(di��n)��
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2�����c(di��n)![]() �P(gu��n)��
�P(gu��n)��![]() �S���Q�c(di��n)���c(di��n)
�S�Č��Q�c(di��n)���c(di��n)![]() ���C����ֱ��
���C����ֱ��![]() �c
�c![]() �S�ཻ�ڶ��c(di��n)��
�S�ཻ�ڶ��c(di��n)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����![]() ��m��R.
��m��R.
(1)��m��3����A��B��
(2)��֪���}p��x��A�����}q��x��B����q��p�ı�Ҫ�l������(sh��)��(sh��)m��ȡֵ������
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com