
已知無窮數列{an}中,a1,a2,…,am是首項為10,公差為-2的等差數列;am+1,
am+2,…,a2m是首項為 ,公比為
,公比為 的等比數列(其中
m≥3,m∈N*),并對任意的n∈N*,均有an+2m=an成立.
的等比數列(其中
m≥3,m∈N*),并對任意的n∈N*,均有an+2m=an成立.
(1)當m=12時,求a2010;
(2)若a52= ,試求m的值;
,試求m的值;
(3)判斷是否存在m(m≥3,m∈N*),使得S128m+3≥2010成立?若存在,試求出m的值;若不存在,請說明理由.
(1)a2010=a18=a12+6=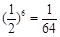 .
.
(2),m=45,或15,或9.
(3)不存在m(m≥3,m∈N*),使得S128m+3≥2010成立.
【解析】解(1)m=12時,數列的周期為24.
∵2010=24×83+18,而a18是等比數列中的項,
∴a2010=a18=a12+6=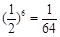 .
.
(2)設am+k是第一個周期中等比數列中的第k項,則am+k=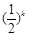 .
.
∵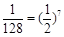 ,∴等比數列中至少有7項,即m≥7,則一個周期中至少有14項.
,∴等比數列中至少有7項,即m≥7,則一個周期中至少有14項.
∴a52最多是第三個周期中的項.
若a52是第一個周期中的項,則a52=am+7= .
.
∴m=52-7=45;
若a52是第二個周期中的項,則a52=a3m+7= .∴3m=45,m=15;
.∴3m=45,m=15;
若a52是第三個周期中的項,則a52=a5m+7= .∴5m=45,m=9;
.∴5m=45,m=9;
綜上,m=45,或15,或9.
(3)2m是此數列的周期,
∴S128m+3表示64個周期及等差數列的前3項之和.
∴S2m最大時,S128m+3最大.
∵S2m=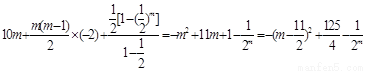 ,
,
當m=6時,S2m=31-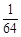 =
=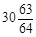 ;
;
當m≤5時,S2m<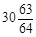 ;
;
當m≤7時,S2m<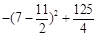 =29<
=29<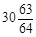 .
.
∴當m=6時,S2m取得最大值,則S128m+3取得最大值為64×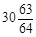 +24=2007.
+24=2007.
由此可知,不存在m(m≥3,m∈N*),使得S128m+3≥2010成立.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:高中數學 來源: 題型:
| 8 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 64 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com