
���}Ŀ��.�O����(bi��o)ϵ��ֱ������(bi��o)ϵ![]() ����ͬ���L(zh��ng)�Ȇ�λ����ԭ�c(di��n)
����ͬ���L(zh��ng)�Ȇ�λ����ԭ�c(di��n)![]() ��O�c(di��n)����
��O�c(di��n)����![]() �����S��O�S.��֪����
�����S��O�S.��֪����![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ������
������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ���侀
���侀![]() ��
��![]() ��
��![]() ��
��![]() �c����
�c����![]() �քe�����ژO�c(di��n)
�քe�����ژO�c(di��n)![]() �����c(di��n)
�����c(di��n)![]() .
.
��1��������![]() �P(gu��n)������
�P(gu��n)������![]() ��(du��)�Q(ch��ng)����
��(du��)�Q(ch��ng)����![]() ��ֵ����������
��ֵ����������![]() ��
��![]() ����ֱ������(bi��o)���̣�
����ֱ������(bi��o)���̣�
��2���O(sh��)![]() ����(d��ng)
����(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ��ֵ��.
��ֵ��.
���𰸡���1��![]() ��
��![]() ��ֱ������(bi��o)���̞�
��ֱ������(bi��o)���̞�![]() ;
;![]() ��ֱ������(bi��o)���̞�
��ֱ������(bi��o)���̞�![]() ;��2��
;��2��![]() .
.
��������
��1����![]() �ɵ�
�ɵ�![]() �M(j��n)������
�M(j��n)������![]() ��ֱ������(bi��o)����; ��
��ֱ������(bi��o)����; ��![]() �ķ��̻���ֱ������(bi��o)���̞�
�ķ��̻���ֱ������(bi��o)���̞�![]() �����}��֪��ԓֱ���^(gu��)
�����}��֪��ԓֱ���^(gu��)![]() ���t�����
���t�����![]() .
.
��2��![]() ��
��![]() ��
��![]() ��
��![]() ���t
���t![]() ���Y(ji��)��
���Y(ji��)��![]() �t�����
�t�����![]() ���M(j��n)������ֵ��.
���M(j��n)������ֵ��.
�⣺��1��![]() ��
��![]() ����
����![]() ������ֱ������(bi��o)����
������ֱ������(bi��o)����
��![]() .��
.��![]() �ķ��̻���ֱ������(bi��o)���̞�
�ķ��̻���ֱ������(bi��o)���̞�![]() .
.
��?y��n)�����![]() �P(gu��n)������
�P(gu��n)������![]() ��(du��)�Q(ch��ng)����ֱ��
��(du��)�Q(ch��ng)����ֱ��![]() ��(j��ng)�^(gu��)�A��
��(j��ng)�^(gu��)�A��![]()
���![]() ����
����![]() ��ֱ������(bi��o)���̞�
��ֱ������(bi��o)���̞�![]() .
.
��2�����}��ɵã���(d��ng)![]() �r(sh��)��
�r(sh��)��
![]() ��
��![]() ��
��![]() ��
��![]()
�t![]()
![]() .
.
��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ���t
���t![]()
��![]() ��ֵ��?y��n)?/span>
��ֵ��?y��n)?/span>![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������ɶ��������������Q(ch��ng)�顰���_(d��)����˹������.����(gu��)�r(sh��)�ڣ��LJ�(gu��)�Ĕ�(sh��)�W(xu��)���wˬ��(chu��ng)����һ�������ɈA���D�����Ô�(sh��)�νY(ji��)�ϵķ����o���˹��ɶ�����Ԕ��(x��)�C��.��D��ʾ�ġ����ɈA���D���У��Ă�(g��)��ͬ��ֱ���������c���g��С������ƴ��һ��(g��)�������Σ���ֱ�����������^С���J��![]() ���F(xi��n)����ԓ�����΅^(q��)���(n��i)�S�C(j��)��Ͷ�S100ö�w�S���t��Ӌ(j��)�w�S���څ^(q��)��1��ö��(sh��)���п����ǣ� ��
���F(xi��n)����ԓ�����΅^(q��)���(n��i)�S�C(j��)��Ͷ�S100ö�w�S���t��Ӌ(j��)�w�S���څ^(q��)��1��ö��(sh��)���п����ǣ� ��
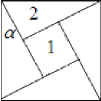
A.30B.40C.50D.60
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() (
(![]() )���x���ʞ�
)���x���ʞ�![]() ����
����![]() �Ķ��S��ֱ���ĈA�cֱ��
�Ķ��S��ֱ���ĈA�cֱ��![]() ����.
����.
��1����![]() �ķ��̣�
�ķ��̣�
��2��ֱ��![]() ��
��![]() ��
��![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() .��֪
.��֪![]() �ϴ����c(di��n)
�ϴ����c(di��n)![]() ��ʹ��
��ʹ��![]() ����
����![]() ��픽ǵĵ���ֱ�������Σ���
��픽ǵĵ���ֱ�������Σ���![]() ��ֱ��
��ֱ��![]() �����·�����
�����·�����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D1����������![]() �У�
��![]() ��
��![]() ��
��![]() �����c(di��n).��
�����c(di��n).��![]() ��
��![]() �������D2��ʹ�����
�������D2��ʹ�����![]() ��ֱ����ǣ��O(sh��)
��ֱ����ǣ��O(sh��)![]() ��
��![]() �����c(di��n)��
�����c(di��n)��![]() ����
����![]() ����
����
�c(di��n).
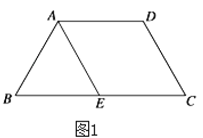

��1�����C��![]() ��
��
��2�����C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��3���Д�![]() �ܷ�ֱ��ƽ��
�ܷ�ֱ��ƽ��![]() �����f(shu��)������.
�����f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1��ӑՓ����(sh��)![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��2��ԇ��(sh��)![]() ���c(di��n)�Ă�(g��)��(sh��)�����C����ĽY(ji��)Փ.
���c(di��n)�Ă�(g��)��(sh��)�����C����ĽY(ji��)Փ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵxOy�У���O��O�c(di��n)��x�S�������S��O�S�������O����(bi��o)ϵ������C�ĘO����(bi��o)���̞���2��cos2��+3sin2������12��ֱ��l�ą���(sh��)���̞�![]() ��t�酢��(sh��)����ֱ��l�c����C����M��N���c(di��n).
��t�酢��(sh��)����ֱ��l�c����C����M��N���c(di��n).
��1�����c(di��n)P�ĘO����(bi��o)�飨2����������|PM||PN|��ֵ��
��2��������C�ă�(n��i)�Ӿ������L(zh��ng)�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��2019���(gu��)�c��(ji��)�������g��ij�̈�(ch��ng)�����ռ������g�ُ(g��u)�I(m��i)��Ʒ�˴Σ��y(t��ng)Ӌ(j��)��10��1��7��00��23��00�@һ�r(sh��)�g��(n��i)�ُ(g��u)�I(m��i)��Ʒ�˴Σ��y(t��ng)Ӌ(j��)�l(f��)�F(xi��n)�@һ�r(sh��)�g��(n��i)�ُ(g��u)�I(m��i)��Ʒ��5000�˴��ُ(g��u)�I(m��i)��Ʒ�r(sh��)�̵ĵ��l�ʷֲ�ֱ���D���D��ʾ�����Еr(sh��)�g��7��0011��00��11��0015��00��15��00��19��00��19��00��23��00������ӛ��[7��11����[11��15����[15��19����[19��23].
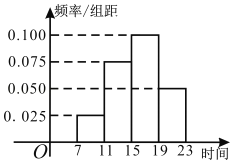
��1����ԓ���ُ(g��u)�I(m��i)��Ʒ�r(sh��)�̵���λ��(sh��)t�cƽ��ֵ![]() ��ͬһ�M�еĔ�(sh��)��(j��)��ԓ�M�^(q��)�g�����c(di��n)ֵ��������
��ͬһ�M�еĔ�(sh��)��(j��)��ԓ�M�^(q��)�g�����c(di��n)ֵ��������
��2�����l�ʷֲ�ֱ���D���Խ����J(r��n)���(gu��)�c��(ji��)�������gԓ�̈�(ch��ng)�ُ(g��u)�I(m��i)��Ʒ�r(sh��)�̷������B(t��i)�ֲ�N��������2�������������ƞ�![]() ������3.6����Ӌ(j��)2019���(gu��)�c��(ji��)�������g��10��1�թ�10��7�գ�ԓ�̈�(ch��ng)���12��12��19��24֮�gُ(g��u)�I(m��i)��Ʒ�Ŀ�?c��)˴Σ��Y(ji��)����������(sh��)����
������3.6����Ӌ(j��)2019���(gu��)�c��(ji��)�������g��10��1�թ�10��7�գ�ԓ�̈�(ch��ng)���12��12��19��24֮�gُ(g��u)�I(m��i)��Ʒ�Ŀ�?c��)˴Σ��Y(ji��)����������(sh��)����
��3������S��(ji��)�՚�գ�ԓ�̈�(ch��ng)����(j��)�}�е�4��(g��)�r(sh��)�g�ηֽM�����÷ӳ�ӵķ������@5000��(g��)�ӱ����S�C(j��)��ȡ10��(g��)�ӱ������O(sh��)�@10��(g��)�ӱ���10��(g��)��ͬͣ��������\(y��n)�͑�����?g��u)��@10��(g��)���\(y��n)�͑����S�C(j��)��ȡ4��ÿ�˪�(ji��ng)��(l��)500Ԫُ(g��u)��ȯ���������\(y��n)�͑�ÿ�˪�(ji��ng)��(l��)200Ԫُ(g��u)��ȯ��ӛ�@��500Ԫُ(g��u)��ȯ��4������15��00��19��00֮�gُ(g��u)�I(m��i)��Ʒ���˔�(sh��)��X����X�ķֲ����c��(sh��)�W(xu��)������
������(sh��)��(j��)����T��N��������2�����t��P����������T�ܦ�+������0.6827����P������2����T�ܦ�+2������0.9545����P������3����T�ܦ�+3������0.9973.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���ĸ��_(k��i)���ԁ�(l��i)���Ї�(gu��)���f�ИI(y��)���m(x��)���ٰl(f��)չ�����f�I(y��)��(w��)���������o(j��)![]() �����
�����![]() �f(w��n)��������2018���
�f(w��n)��������2018���![]() �|�������f�ИI(y��)�İl(f��)չҲ�o�҂��������(l��i)�˺ܴ����.��֪ij��ij���f�c(di��n)�����M(f��i)��(bi��o)��(zh��n)��:����(����С�ڵ���
�|�������f�ИI(y��)�İl(f��)չҲ�o�҂��������(l��i)�˺ܴ����.��֪ij��ij���f�c(di��n)�����M(f��i)��(bi��o)��(zh��n)��:����(����С�ڵ���![]() )���M(f��i)
)���M(f��i)![]() Ԫ���m(x��)��
Ԫ���m(x��)��![]() Ԫ
Ԫ![]() (����
(����![]() ��
��![]() ��). (��:һ��(g��)����������
��). (��:һ��(g��)����������![]() �t��֧����
�t��֧����![]() Ԫ���m(x��)��
Ԫ���m(x��)��![]() Ԫ��һ��
Ԫ��һ��![]() Ԫ���f�M(f��i)��)
Ԫ���f�M(f��i)��)
��1�������������Y��![]() �����քe��
�����քe��![]() ��Ҫ������(g��)�Y��ֳɃɂ�(g��)�����ij�(��:
��Ҫ������(g��)�Y��ֳɃɂ�(g��)�����ij�(��:![]() �Ϟ�һ��(g��)������
�Ϟ�һ��(g��)������![]() һ��(g��)����)����ô��η���Y�ʹ���㻨�M(f��i)�Ŀ��f�M(f��i)���٣�
һ��(g��)����)����ô��η���Y�ʹ���㻨�M(f��i)�Ŀ��f�M(f��i)���٣�
��2����(du��)ԓ���f�c(di��n)��![]() ���ÿ�Ք�������(sh��)(��λ:��)�M(j��n)�нy(t��ng)Ӌ(j��)���õ����Ք�������(sh��)�քe��
���ÿ�Ք�������(sh��)(��λ:��)�M(j��n)�нy(t��ng)Ӌ(j��)���õ����Ք�������(sh��)�քe��![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() �������@
�������@![]() �����S�C(j��)���
�����S�C(j��)���![]() �죬���@
�죬���@![]() ����Ք�������(sh��)�����^(gu��)
����Ք�������(sh��)�����^(gu��)![]() ���ĸ���.
���ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ���x���ʞ�
���x���ʞ�![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)��![]() ����ԭ�c(di��n)
����ԭ�c(di��n)![]() ��A�ģ��E�A
��A�ģ��E�A![]() �Ķ̰��S�L(zh��ng)��돽�ĈA�cֱ��
�Ķ̰��S�L(zh��ng)��돽�ĈA�cֱ��![]() ����.
����.

��1����E�A![]() �ķ��̣�
�ķ��̣�
��2����D���^(gu��)���c(di��n)![]() ��ֱ��
��ֱ��![]() ���E�A
���E�A![]() ��
��![]() ���c(di��n)���B��
���c(di��n)���B��![]() �����L(zh��ng)��
�����L(zh��ng)��![]() ��
��![]() �����C��
�����C��![]() .
.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com