
已知函數(shù)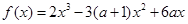
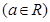 .
.
(1)當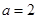 時,求函數(shù)
時,求函數(shù)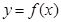 的單調區(qū)間;
的單調區(qū)間;
(2)若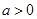 時,函數(shù)
時,函數(shù)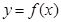 在閉區(qū)間
在閉區(qū)間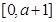 上的最大值為
上的最大值為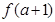 ,求
,求 的取值范圍.
的取值范圍.
(1)單調增區(qū)間分別為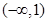 ,
,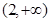 ,單調減區(qū)間為
,單調減區(qū)間為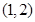 ;(2)
;(2)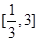 .
.
解析試題分析:本題主要考查導數(shù)的運算,利用導數(shù)研究函數(shù)的單調性、極值、最值以及不等式的基礎知識,考查分類討論思想,考查綜合運用數(shù)學知識和方法分析問題解決問題的能力和計算能力.第一問,當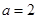 時,函數(shù)解析式中沒有參數(shù),直接求導,令導數(shù)大于0和小于0,分別解出函數(shù)的單調增區(qū)間和單調減區(qū)間;第二問,因為
時,函數(shù)解析式中沒有參數(shù),直接求導,令導數(shù)大于0和小于0,分別解出函數(shù)的單調增區(qū)間和單調減區(qū)間;第二問,因為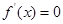 的兩個根是
的兩個根是 和1,所以需要討論
和1,所以需要討論 和1的大小,分3種情況進行討論,分別列表判斷函數(shù)的單調性、極值、最值,求出函數(shù)在閉區(qū)間
和1的大小,分3種情況進行討論,分別列表判斷函數(shù)的單調性、極值、最值,求出函數(shù)在閉區(qū)間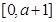 上的最大值判斷是否等于
上的最大值判斷是否等于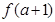 ,求出
,求出 的取值范圍.
的取值范圍.
試題解析: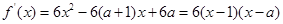 2分
2分
(1)當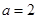 時,
時,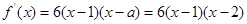
當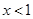 或
或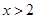 時,
時,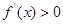 ,
,
當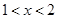 ,
,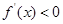 ,
,
所以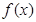 的單調增區(qū)間分別為
的單調增區(qū)間分別為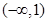 ,
,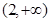 , 5分
, 5分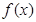 的單調減區(qū)間為
的單調減區(qū)間為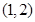 .
.
(2)(Ⅰ)當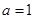 時,
時, ,
,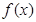 在
在 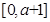 上單調遞增,最大值為
上單調遞增,最大值為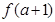
(Ⅱ)當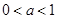 時,列表如下:
時,列表如下: