
【題目】設(shè)函數(shù)f(x)=sin(2x+φ)(-π<φ<0),y=f(x)圖象的一條對(duì)稱軸是直線![]()
(1)求φ;
(2)求函數(shù)y=f(x)的單調(diào)遞增區(qū)間;
(3)求函數(shù)y=f(x)在區(qū)間![]() 上的值域。
上的值域。
【答案】(1) ![]() ;(2)[kπ+
;(2)[kπ+![]() ,kπ+
,kπ+![]() ],k∈z.(3)[-1,
],k∈z.(3)[-1, ![]() ].
].
【解析】試題分析:
(1)由函數(shù)的對(duì)稱軸可得![]() ;
;
(2)結(jié)合函數(shù)的解析式可得函數(shù)的單調(diào)遞增區(qū)間為![]() ,
,
(3)結(jié)合三角函數(shù)的性質(zhì)可得函數(shù)的值域?yàn)?/span>[-1, ![]() ].
].
試題解析:
(1)由于函數(shù)f(x)=sin(2x+φ)(-π<φ<0)的圖象的一條對(duì)稱軸是直線x=![]() ,
,
可得2×![]() +φ=kπ+
+φ=kπ+![]() ,求得φ=kπ+
,求得φ=kπ+![]() ,k∈z,∴φ=
,k∈z,∴φ=![]() .
.
(2)令2kπ-![]() 2x
2x![]() 2kπ+
2kπ+![]() ,k∈z,求得kπ+
,k∈z,求得kπ+![]() xkπ+
xkπ+![]() ,
,
可得函數(shù)y=f(x)的單調(diào)遞增區(qū)間為[kπ+![]() ,kπ+
,kπ+![]() ],k∈z.
],k∈z.
由x∈[![]() ,
,![]() ],可得2x
],可得2x![]() ∈[
∈[![]() ,
,![]()
![]() ].
].


 培優(yōu)好卷單元加期末卷系列答案
培優(yōu)好卷單元加期末卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() 經(jīng)過點(diǎn)A
經(jīng)過點(diǎn)A![]() ,求:
,求:
(1)直線![]() 在兩坐標(biāo)軸上的截距相等的直線方程;
在兩坐標(biāo)軸上的截距相等的直線方程;
(2)直線![]() 與兩坐標(biāo)軸的正半軸圍成三角形面積最小時(shí)的直線方程.
與兩坐標(biāo)軸的正半軸圍成三角形面積最小時(shí)的直線方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形ABCD為正方形, ![]() 為直角三角形,
為直角三角形, ![]() ,且
,且![]() .
.
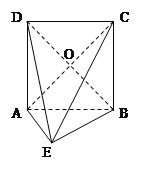
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若AB=2AE,求異面直線BE與AC所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61,
(1)求a與b的夾角θ; (2)求|a+b|;
(3)若![]() =a,
=a, ![]() =b,求△ABC的面積.
=b,求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國上是世界嚴(yán)重缺水的國家,城市缺水問題較為突出,某市政府為了鼓勵(lì)居民節(jié)約用水,計(jì)劃在本市試行居民生活用水定額管理,即確定一個(gè)合理的居民月用水量標(biāo)準(zhǔn)![]() (噸),用水量不超過
(噸),用水量不超過![]() 的部分按平價(jià)收費(fèi),超過
的部分按平價(jià)收費(fèi),超過![]() 的部分按議價(jià)收費(fèi),為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數(shù)據(jù)按照
的部分按議價(jià)收費(fèi),為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數(shù)據(jù)按照![]() ,
, ![]() ,…,
,…, ![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
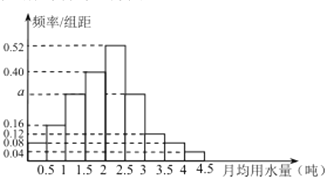
(Ⅰ)求直方圖中![]() 的值;
的值;
(Ⅱ)已知該市有80萬居民,估計(jì)全市居民中月均用水量不低于3噸的人數(shù),并說明理由;
(Ⅲ)若該市政府希望使![]() 的居民每月的用水量不超過標(biāo)準(zhǔn)
的居民每月的用水量不超過標(biāo)準(zhǔn)![]() (噸),估計(jì)
(噸),估計(jì)![]() 的值,并說明理由;
的值,并說明理由;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)樣本x1,x2,…,x10數(shù)據(jù)的平均值和方差分別為3和5,若yi=xi+a(a為非零實(shí)數(shù),i=1,2,…,10),則y1,y2,…,y10的均值和方差分別為( )
A. 3,5 B. 3+a,5 C. 3+a,5+a D. 3,5+a
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)若曲線![]() 在點(diǎn)
在點(diǎn)![]() 處與直線
處與直線![]() 相切,求
相切,求![]() 的值;
的值;
(2)若函數(shù)![]() 有兩個(gè)零點(diǎn)
有兩個(gè)零點(diǎn)![]() ,
,![]() ,試判斷
,試判斷![]() 的符號(hào),并證明.
的符號(hào),并證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 為數(shù)列
為數(shù)列![]() 的前
的前![]() 項(xiàng)和,對(duì)任意的
項(xiàng)和,對(duì)任意的![]() ,都有
,都有![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足![]() ,
, ![]() .
.
(1)求證:數(shù)列![]() 是等比數(shù)列,并求
是等比數(shù)列,并求![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(3)求數(shù)列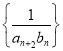 的前
的前![]() 項(xiàng)和
項(xiàng)和![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若存在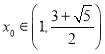 ,使函數(shù)
,使函數(shù)![]() 的圖像在點(diǎn)
的圖像在點(diǎn)![]() 和點(diǎn)
和點(diǎn)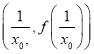 處的切線互相垂直,求
處的切線互相垂直,求![]() 的取值范圍;
的取值范圍;
(3)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上有兩個(gè)極值點(diǎn),則是否存在實(shí)數(shù)
上有兩個(gè)極值點(diǎn),則是否存在實(shí)數(shù)![]() ,使
,使![]() 對(duì)任意的
對(duì)任意的![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范圍,若不存在,說明理由.
的取值范圍,若不存在,說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com