
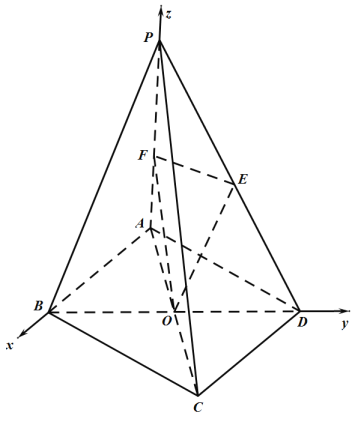
【題目】如圖在四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 為等腰直角三角形,且
為等腰直角三角形,且![]() ,
,![]() 為底面
為底面![]() 的中心.
的中心.
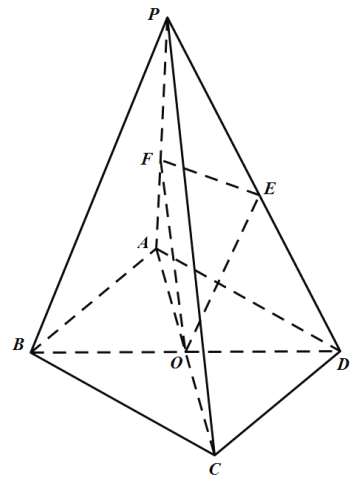
(1)求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(2)若![]() 為
為![]() 中點,
中點,![]() 在棱
在棱![]() 上,若
上,若![]() ,
,![]() ,且二面角
,且二面角![]() 的正弦值為
的正弦值為![]() ,求實數(shù)
,求實數(shù)![]() 的值.
的值.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)根據面![]() 面
面![]() ,
,![]() ,得到
,得到![]() 面
面![]() ,以
,以![]() 為原點建立空間直角坐標系,得到
為原點建立空間直角坐標系,得到![]() ,
,![]() 的坐標,根據向量夾角公式,得到異面直線
的坐標,根據向量夾角公式,得到異面直線![]() 與
與![]() 所成角的余弦值;(2)設
所成角的余弦值;(2)設![]() ,從而得到
,從而得到![]() 點坐標,結合(1)取平面
點坐標,結合(1)取平面![]() 的法向量
的法向量![]() ,求出平面
,求出平面![]() 的法向量為
的法向量為![]() ,通過法向量表示出二面角
,通過法向量表示出二面角![]() 的余弦值,根據其正弦值為
的余弦值,根據其正弦值為![]() ,列出關于
,列出關于![]() 的方程,求出
的方程,求出![]() 的值.
的值.
(1)∵![]() 為等腰直角三角形,
為等腰直角三角形,
∴![]() ,
,
∵面![]() 面
面![]() ,
,
面![]() 面
面![]() ,
,![]() 面
面![]()
∴![]() 面
面![]() ,
,
∵底面![]() 為矩形, 所以
為矩形, 所以![]() ,
,![]() ,
,![]() 三條線兩兩垂直.
三條線兩兩垂直.
以![]() 為原點,
為原點,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 軸建立空間直角坐標系,
軸建立空間直角坐標系,
知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
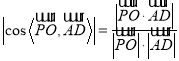
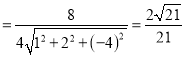 ,
,
所以異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() .
.
(2)結合(1)知![]() ,
,![]() 面
面![]() ,
,
取平面![]() 的法向量
的法向量![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
又![]() ,
,![]() ,
,
 ,即
,即![]() ,
,
令![]() ,得
,得![]() ,
,
又因為二面角![]() 的正弦值為
的正弦值為![]() ,
,
所以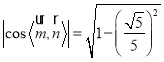 ,
,
而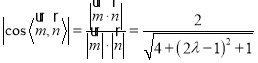 ,
,
即 ,
,
解得![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】自貢農科所實地考察,研究發(fā)現(xiàn)某貧困村適合種植![]() ,
,![]() 兩種藥材,可以通過種植這兩種藥材脫貧.通過大量考察研究得到如下統(tǒng)計數(shù)據:藥材
兩種藥材,可以通過種植這兩種藥材脫貧.通過大量考察研究得到如下統(tǒng)計數(shù)據:藥材![]() 的畝產量約為300公斤,其收購價格處于上漲趨勢,最近五年的價格如下表:
的畝產量約為300公斤,其收購價格處于上漲趨勢,最近五年的價格如下表:
編號 | 1 | 2 | 3 | 4 | 5 |
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
單價(元/公斤) | 18 | 20 | 23 | 25 | 29 |
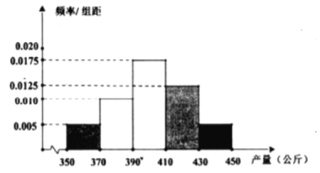
藥材![]() 的收購價格始終為20元/公斤,其畝產量的頻率分布直方圖如下:
的收購價格始終為20元/公斤,其畝產量的頻率分布直方圖如下:
(1)若藥材![]() 的單價
的單價![]() (單位:元/公斤)與年份編號
(單位:元/公斤)與年份編號![]() 具有線性相關關系,請求出
具有線性相關關系,請求出![]() 關于
關于![]() 的回歸直線方程,并估計2020年藥材
的回歸直線方程,并估計2020年藥材![]() 的單價;
的單價;
(2)用上述頻率分布直方圖估計藥材![]() 的平均畝產量,若不考慮其他因素,試判斷2020年該村應種植藥材
的平均畝產量,若不考慮其他因素,試判斷2020年該村應種植藥材![]() 還是藥材
還是藥材![]() ?并說明理由.
?并說明理由.
參考公式: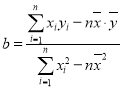 ,
,![]() (回歸方程
(回歸方程![]() 中)
中)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 在
在![]() 上單調遞減,求
上單調遞減,求![]() 的取值范圍;
的取值范圍;
(2)若![]() 在
在![]() 處取得極值,判斷當
處取得極值,判斷當![]() 時,存在幾條切線與直線
時,存在幾條切線與直線![]() 平行,請說明理由;
平行,請說明理由;
(3)若![]() 有兩個極值點
有兩個極值點![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的焦距為4,其短軸的兩個端點與長軸的一個端點構成正三角形.
)的焦距為4,其短軸的兩個端點與長軸的一個端點構成正三角形.
(1)求橢圓C的標準方程;
(2)設F為橢圓C的左焦點,T為直線![]() 上任意一點,過F作TF的垂線交橢圓C于點P,Q.
上任意一點,過F作TF的垂線交橢圓C于點P,Q.
(i)證明:OT平分線段PQ(其中O為坐標原點);
(ii)當![]() 最小時,求點T的坐標.
最小時,求點T的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在單位正方體![]() 中,點P在線段
中,點P在線段![]() 上運動,給出以下四個命題:
上運動,給出以下四個命題:

![]() 異面直線
異面直線![]() 與
與![]() 間的距離為定值;
間的距離為定值;
![]() 三棱錐
三棱錐![]() 的體積為定值;
的體積為定值;
![]() 異面直線
異面直線![]() 與直線
與直線![]() 所成的角為定值;
所成的角為定值;
![]() 二面角
二面角![]() 的大小為定值.
的大小為定值.
其中真命題有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),以坐標原點為極點,
為參數(shù)),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,點
,點![]() 的極坐標為
的極坐標為![]() .
.
(1)求![]() 的直角坐標方程和
的直角坐標方程和![]() 的直角坐標;
的直角坐標;
(2)設![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】影響消費水平的原因很多,其中重要的一項是工資收入.研究這兩個變量的關系的一個方法是通過隨機抽樣的方法,在一定范圍內收集被調查者的工資收入和他們的消費狀況.下面的數(shù)據是某機構收集的某一年內上海、江蘇、浙江、安徽、福建五個地區(qū)的職工平均工資與城鎮(zhèn)居民消費水平(單位:萬元).
地區(qū) | 上海 | 江蘇 | 浙江 | 安徽 | 福建 |
職工平均工資 | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
城鎮(zhèn)居民消費水平 | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
(1)利用江蘇、浙江、安徽三個地區(qū)的職工平均工資和他們的消費水平,求出線性回歸方程![]() ,其中
,其中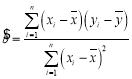
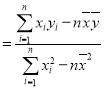 ,
,![]() ;
;
(2)若由線性回歸方程得到的估計數(shù)據與所選出的檢驗數(shù)據的誤差均不超過1萬,則認為得到的線性回歸方程是可靠的,試問所得的線性回歸方程是否可靠?(![]() 的結果保留兩位小數(shù))
的結果保留兩位小數(shù))
(參考數(shù)據:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨著社會的進步,經濟的發(fā)展,道路上的汽車越來越多,隨之而來的交通事故也增多.據有關部門調查,發(fā)生車禍的駕駛員中尤其是21 歲以下年輕人所占比例居高,因此交通管理有關部門,對2018 年參加駕照考試的21 歲以下學員隨機抽取10 名學員,對他們參加的科目三(道路駕駛)和科目四(安全文明駕駛相關知識)進行兩輪現(xiàn)場測試,并把兩輪測試成績的平均分作為該名學員的抽測成績.記錄的數(shù)據如下:
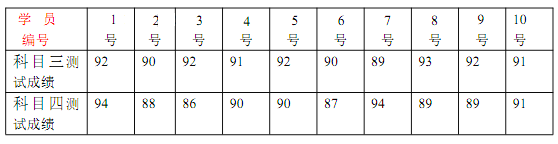
(1)從2018年參加駕照考試的21歲以下學員中隨機選取一名學員,試估計這名學員抽測成績大于或等于90分的概率;
(2)根據規(guī)定,科目三和科目四測試成績均達到90分以上(含90)才算測試合格.
(i)從抽測的1號至5號學員中任取兩名學員,記![]() 為學員測試合格的人數(shù),求
為學員測試合格的人數(shù),求![]() 的分布列和數(shù)學期望
的分布列和數(shù)學期望![]() ;
;
(ii) 記抽取的10名學員科目三和科目四測試成績的方差分別為![]() ,
,![]() ,試比較
,試比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com