
已知函數![]() 的最大值不大于
的最大值不大于![]() ,又當
,又當![]()
(1)求a的值;
(2)設![]()
(1)解:由于![]() 的最大值不大于
的最大值不大于![]() 所以
所以
![]() ① ………………3分
① ………………3分
又![]() 所以
所以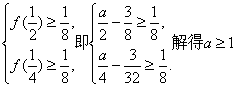 . ②
. ②
由①②得![]() ………………6分
………………6分
(2)證法一:(i)當n=1時,![]() ,不等式
,不等式![]() 成立;
成立;
因![]() 時不等式也成立.
時不等式也成立.
(ii)假設![]() 時,不等式
時,不等式![]() 成立,因為
成立,因為![]() 的
的
對稱軸為![]() 知
知![]() 為增函數,所以由
為增函數,所以由![]() 得
得
![]() ………………8分
………………8分
于是有
![]()
…………12分
所以當n=k+1時,不等式也成立.
根據(i)(ii)可知,對任何![]() ,不等式
,不等式![]() 成立.…………14分
成立.…………14分
證法二:(i)當n=1時,![]() ,不等式
,不等式![]() 成立;
成立;
(ii)假設![]() 時不等式成立,即
時不等式成立,即![]() ,則當n=k+1時,
,則當n=k+1時,
![]() ………………8分
………………8分
因![]() 所以
所以
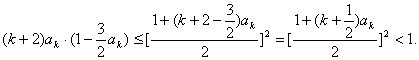 ……12分
……12分
于是![]() 因此當n=k+1時,不等式也成立.
因此當n=k+1時,不等式也成立.
根據(i)(ii)可知,對任何![]() ,不等式
,不等式![]() 成立.…………14分
成立.…………14分


 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com