
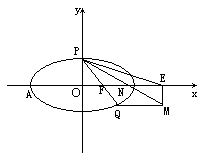
��D���E�A���̞�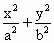 ��1(a��b��0)��A��P��F(xi��n)�քe������c(di��n)������c(di��n)���ҽ��c(di��n)��E��x�S�������ϵ�һ�c(di��n)����|
��1(a��b��0)��A��P��F(xi��n)�քe������c(di��n)������c(di��n)���ҽ��c(di��n)��E��x�S�������ϵ�һ�c(di��n)����| |��|
|��| |��|
|��| |�ɵȱȔ�(sh��)�У����c(di��n)N�M��
|�ɵȱȔ�(sh��)�У����c(di��n)N�M�� ��
��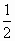 (
(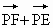 )��PF�����L���c�E�A�Ľ��c(di��n)��Q���^Q�cx�Sƽ�е�ֱ���cPN�����L������M��
)��PF�����L���c�E�A�Ľ��c(di��n)��Q���^Q�cx�Sƽ�е�ֱ���cPN�����L������M��
(1)���C��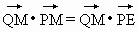 ��
��
(2)��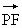 ��2
��2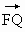 ����|
����| |��
|�� ����E�A�ķ��̣�
����E�A�ķ��̣�
|
�����⡡��(1)�O(sh��)E(x0��0)����| ���� ����PF����ֱ�����̞� ������y�� ������PN�ķ��̞� ������EM��x�S���� ����(2) ������ ������ |


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ���O(sh��)Ӌ(j��)�x�ޔ�(sh��)�W(xu��)��1-1�K�̰� �K�̰� �}�ͣ�044
�W(xu��)У�Ƽ�С�M��Ӌ(j��)��C(j��)��ģ�M������׃܉����ԇ�(y��n)���O(sh��)Ӌ(j��)������D244��ʾ���������\(y��n)��(��형rᘷ���)��܉�E���̞�![]() ��1��׃܉(���������\(y��n)��܉�E�əE�A׃?y��u)钁�タ)�ص�܉�E����y�S�錦�Q�S��M(0��
��1��׃܉(���������\(y��n)��܉�E�əE�A׃?y��u)钁�タ)�ص�܉�E����y�S�錦�Q�S��M(0��![]() )����c(di��n)�Ē��タ�Č�(sh��)�����֣������c(di��n)��D(8��0)���^�y�c(di��n)A(4��0)��B(6��0)ͬ�r��ۙ��������
)����c(di��n)�Ē��タ�Č�(sh��)�����֣������c(di��n)��D(8��0)���^�y�c(di��n)A(4��0)��B(6��0)ͬ�r��ۙ��������
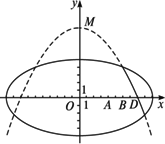
(1)������׃܉����\(y��n)��܉�E���ڵ��������̣�
(2)ԇ������(d��ng)��������x�S�Ϸ��r���^�y�c(di��n)A��B�y���x�������ľ��x�քe����ٕr����(y��ng)�������l(f��)��׃܉ָ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2010����ͨ�ߵȌW(xu��)У����ȫ���y(t��ng)һ��ԇ�����Ɣ�(sh��)�W(xu��)(�����) �}�ͣ�044
��D���E�AC��![]() ��1����c(di��n)��A1��A2��B1��B2�����c(di��n)��F1��F(xi��n)2��|A1B1|��
��1����c(di��n)��A1��A2��B1��B2�����c(di��n)��F1��F(xi��n)2��|A1B1|��![]() ��
��![]() ��2
��2![]() ��
��
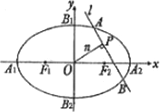
(��)��E�AC�ķ��̣�
(��)�O(sh��)n���^ԭ�c(di��n)��ֱ����l���cn��ֱ�ཻ��P�c(di��n)���c�E�A�ཻ��A��B���c(di��n)��ֱ����|![]() |��1���Ƿ��������ֱ��lʹ
|��1���Ƿ��������ֱ��lʹ![]() ��
��![]() ��1�����������ڣ����ֱ��l�ķ��̣��������ڣ�Ո�f�����ɣ�
��1�����������ڣ����ֱ��l�ķ��̣��������ڣ�Ո�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2012����ͨ�ߵȌW(xu��)У����ȫ���y(t��ng)һ��ԇ�����픵(sh��)�W(xu��)���� �}�ͣ�044
��D���E�AE��![]() ��1(a��b��0)�����c(di��n)��F1���ҽ��c(di��n)��F2���x����e��
��1(a��b��0)�����c(di��n)��F1���ҽ��c(di��n)��F2���x����e��![]() ���^F1��ֱ�����E�A��A��B���c(di��n)���ҡ�ABF2�����L��8��
���^F1��ֱ�����E�A��A��B���c(di��n)���ҡ�ABF2�����L��8��
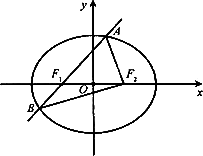
(��)��E�AE�ķ��̣�
(��)�O(sh��)��ֱ��l��y��kx��m�c�E�AE����ֻ��һ�������c(di��n)P�����cֱ��x��4���^���c(di��n)Q��ԇ̽����������(bi��o)ƽ���(n��i)�Ƿ���ڶ��c(di��n)M��ʹ����PQ��ֱ���ĈA���^�c(di��n)M�������ڣ�����c(di��n)M������(bi��o)���������ڣ��f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
20.
�W(xu��)У�Ƽ�С�M��Ӌ(j��)��C(j��)��ģ�M������׃܉����ԇ�(y��n)���O(sh��)Ӌ(j��)������D���������\(y��n)�У���형rᘷ���܉�E���̞�![]() ��1��׃܉(���������\(y��n)��܉�E�əE�A׃?y��u)钁�タ)�ص�܉�E����y�S�錦�Q�S��
��1��׃܉(���������\(y��n)��܉�E�əE�A׃?y��u)钁�タ)�ص�܉�E����y�S�錦�Q�S��
M(0,![]() )����c(di��n)�Ē��タ�Č�(sh��)������,�����c(di��n)��D(8,0).�^�y�c(di��n)A(4,0)��B(6,0)ͬ�r��ۙ��������
)����c(di��n)�Ē��タ�Č�(sh��)������,�����c(di��n)��D(8,0).�^�y�c(di��n)A(4,0)��B(6,0)ͬ�r��ۙ��������
(1)������׃܉����\(y��n)��܉�E���ڵ��������̣�
(2)ԇ������(d��ng)��������x�S�Ϸ��r���^�y�c(di��n)A��B�y���x�������ľ��x�քe����ٕr����(y��ng)�������l(f��)��׃܉ָ�

�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com