
���}Ŀ����ֱ֪��![]() �^�E�A
�^�E�A![]() ���ҽ��c(di��n)���ҽ��E�A��A��B���c(di��n)������AB�����c(di��n)��
���ҽ��c(di��n)���ҽ��E�A��A��B���c(di��n)������AB�����c(di��n)��![]() ��
��
��1����E�A�ķ��̣�
��2���^ԭ�c(di��n)��ֱ��l�c����AB�ཻ���������c(di��n)���ҽ��E�A��C��D���c(di��n)������߅��![]() ��e�����ֵ.
��e�����ֵ.
���𰸡���1��![]() ��2��
��2��![]()
��������
��1����ֱ��![]() �ɵÙE�A�ҽ��c(di��n)������(bi��o)��
�ɵÙE�A�ҽ��c(di��n)������(bi��o)��![]() ,�����c(di��n)
,�����c(di��n)![]() �ɵ�
�ɵ�![]() ,����б�ʹ�ʽ�ɵ�
,����б�ʹ�ʽ�ɵ�![]() ,���c(di��n)
,���c(di��n)![]() �ڙE�A��,�t
�ڙE�A��,�t![]() ,��������,�M(j��n)�����������ɵ�
,��������,�M(j��n)�����������ɵ�![]() ,������⣻
,������⣻
��2���O(sh��)ֱ��![]() ,�c(di��n)
,�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x��
�ľ��x��![]() ,�t��߅�ε���e��
,�t��߅�ε���e��![]() ,��
,��![]() ����E�A����,���������L��ʽ���
����E�A����,���������L��ʽ���![]() ,�����c(di��n)��ֱ�����x���
,�����c(di��n)��ֱ�����x���![]() ,����(j��)ֱ��l�c����AB���������c(di��n)���ཻ,�ɵ�
,����(j��)ֱ��l�c����AB���������c(di��n)���ཻ,�ɵ�![]() ,��
,��![]() ,�M(j��n)������QԪ,�ɶ��κ���(sh��)���|(zh��)�����ֵ����.
,�M(j��n)������QԪ,�ɶ��κ���(sh��)���|(zh��)�����ֵ����.
��1��ֱ��![]() �cx�S�����c(di��n)
�cx�S�����c(di��n)![]() ,���ԙE�A�ҽ��c(di��n)������(bi��o)��
,���ԙE�A�ҽ��c(di��n)������(bi��o)��![]() ,��
,��![]() ,
,
��?y��n)龀��AB�����c(di��n)��![]() ,
,
�O(sh��)![]() ,�t
,�t![]() ,��
,��![]() ,
,
��![]() ,����ɵ�
,����ɵ�![]() ,
,
�t![]() ,��
,��![]()
��![]() ,
,
����![]() ,
,
��˙E�A�ķ��̞�![]() .
.
��2���ɣ�1��(li��n)�� ,���
,���![]() ��
��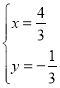 ,
,
������![]() ,��ֱ֪��l��б�ʴ���,
,��ֱ֪��l��б�ʴ���,
�O(sh��)ֱ��![]() ,����
,����![]() ,��
,��![]() ,
,
���![]() ��
��![]() ,
,
�O(sh��)![]() ,�t
,�t![]() ,
,
�t![]() ,
,
��?y��n)?/span>![]() ��ֱ��
��ֱ��![]() �ľ��x�քe��
�ľ��x�քe�� ,
,
����ֱ��l�c����AB���������c(di��n)���ཻ,����![]() ,��
,��![]() ,
,
����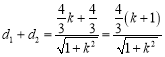 ,
,
��߅��![]() ����e
����e![]() ,
,
��![]() ,
,![]() ,�t
,�t![]() ,
,
����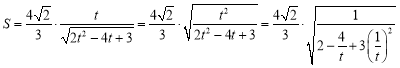 ,
,
��(d��ng)![]() ,��
,��![]() �r(sh��),
�r(sh��), ��
��
�����߅��![]() ��e�����ֵ��
��e�����ֵ��![]() .
.



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ��߅�L��a�Ŀ��g��߅��ABCD�У���BCD��90�㣬ƽ��ABD��ƽ��BCD���t����ֱ��AD�cBC���ɽǵĴ�С�飨������
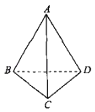
A. 30��B. 45��C. 60��D. 90��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D�����F![]() �У�
��![]() ����
����![]() ��
��![]() ��߅�L��2�ĵ�߅�����Σ���
��߅�L��2�ĵ�߅�����Σ���![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ����
����![]() �ϵĄ��c(di��n).
�ϵĄ��c(di��n).
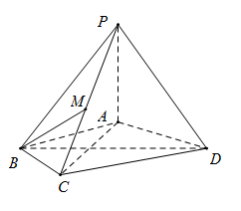
��I�����C��ƽ��![]() ƽ��
ƽ��![]() ��
��
����(d��ng)����![]() ��С�r(sh��)����ֱ��
��С�r(sh��)����ֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����![]() �����c(di��n)�����{(di��o)�^(q��)�g��
�����c(di��n)�����{(di��o)�^(q��)�g��
��2�����C������![]() ����б�ʞ�8���о��������c(di��n)�Ŀv����(bi��o)
����б�ʞ�8���о��������c(di��n)�Ŀv����(bi��o)![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У���ԭ�c(di��n)
�У���ԭ�c(di��n)![]() ��O�c(di��n)��
��O�c(di��n)��![]() �S�����S��O�S�����O����(bi��o)ϵ����ֱ֪��
�S�����S��O�S�����O����(bi��o)ϵ����ֱ֪��![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ������
������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ��
��
��1������ֱ��![]() ������
������![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2���^���c(di��n)![]() ��ƽ����
��ƽ����![]() ��ֱ��������
��ֱ��������![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ������c(di��n)
������c(di��n)![]() ��ֱ��
��ֱ��![]() ��������x��
��������x��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������D��ʾ�������w�У���![]() ��ֱ�����Σ�
��ֱ�����Σ� ![]() ,ƽ��
,ƽ��![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() ��߅�L��2����������.
��߅�L��2����������.
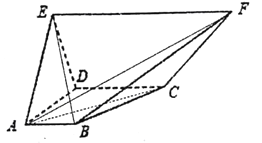
��1���C���� ![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ���c(di��n)
���c(di��n)![]() ��
��![]() ��
��![]() �քe��E�A�����c(di��n)������c(di��n)������c(di��n)��
�քe��E�A�����c(di��n)������c(di��n)������c(di��n)��![]() ����e��
����e��![]() ���ҙE�A���x���ʞ�
���ҙE�A���x���ʞ�![]() .
.
��1����E�A�Ę�(bi��o)��(zh��n)���̣�
��2�����c(di��n)![]() ��E�A
��E�A![]() ��һ�c(di��n)��ֱ��
��һ�c(di��n)��ֱ��![]() �c�E�A
�c�E�A![]() ���ڲ�ͬ�ă��c(di��n)
���ڲ�ͬ�ă��c(di��n)![]() ��
��![]() ����
����![]() ���c(di��n)
���c(di��n)![]() ������(bi��o)ԭ�c(di��n)������
������(bi��o)ԭ�c(di��n)������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��
��![]() ��
��![]() ���o��������(g��)���}����
���o�������Ă�(g��)���}����![]() ��ż����(sh��)����
��ż����(sh��)����![]() ��ż����(sh��)����
��ż����(sh��)����![]() ����Сֵ��0����
����Сֵ��0����![]() �Ѓɂ�(g��)���c(di��n)�����������}���ǣ� ����
�Ѓɂ�(g��)���c(di��n)�����������}���ǣ� ����
A.�ڢ�B.�٢�C.�٢ۢ�D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() .
.
(1)����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ȡ�ØOֵ����
ȡ�ØOֵ����![]() ��ֵ������
��ֵ������![]() �Ć��{(di��o)�^(q��)�g.
���{(di��o)�^(q��)�g.
(2)��![]() ���ڃɂ�(g��)�Oֵ�c(di��n)
���ڃɂ�(g��)�Oֵ�c(di��n)![]() ����
����![]() ��ȡֵ���������C����
��ȡֵ���������C����![]() .
.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com