
【題目】如圖,在棱長均為![]() 的三棱柱
的三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 為
為![]() 與
與![]() 的交點(diǎn).
的交點(diǎn).
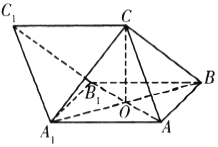
(1)求證:![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
【答案】(1)詳見解析;(2)![]() .
.
【解析】
(1)證明線垂直面,即![]() 平面
平面![]() ,從而證明線線垂直;
,從而證明線線垂直;
(2)以![]() 為坐標(biāo)原點(diǎn),以
為坐標(biāo)原點(diǎn),以![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立如圖所示的空間直角坐標(biāo)系
軸,建立如圖所示的空間直角坐標(biāo)系![]() ,求出平面
,求出平面![]() 與平面
與平面![]() 的法向量,再求出法向量夾角的余弦值,進(jìn)而得到二面角的余弦值.
的法向量,再求出法向量夾角的余弦值,進(jìn)而得到二面角的余弦值.
(1)因?yàn)樗倪呅?/span>![]() 為菱形,所以
為菱形,所以![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因?yàn)?/span>![]() 平面
平面![]() ,
,
所以![]() .
.
(2)因?yàn)?/span>![]() ,所以菱形
,所以菱形![]() 為正方形,
為正方形,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以,![]() ,又
,又![]() ,
,![]() ,
,
所以,![]() 平面
平面![]() ;
;
以![]() 為坐標(biāo)原點(diǎn),以
為坐標(biāo)原點(diǎn),以![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立如圖所示的空間直角坐標(biāo)系
軸,建立如圖所示的空間直角坐標(biāo)系![]() .
.
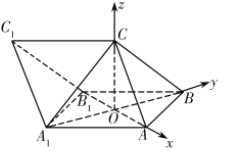
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設(shè)平面![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() 平面
平面![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() ,則
,則
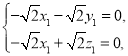
令![]() ,得
,得![]() ,
,

令![]() ,得
,得![]() ,
,
設(shè)平面![]() 與平面
與平面![]() 所成銳二面角為
所成銳二面角為![]() ,
,
則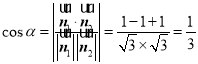 ,
,
所以平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() ,
,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
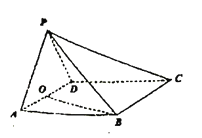
(1)求證:![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某飛機(jī)失聯(lián),經(jīng)衛(wèi)星偵查,其最后出現(xiàn)在小島![]() 附近,現(xiàn)派出四艘搜救船
附近,現(xiàn)派出四艘搜救船![]() ,為方便聯(lián)絡(luò),船
,為方便聯(lián)絡(luò),船![]() 始終在以小島
始終在以小島![]() 為圓心,100海里為半徑的圓上,船
為圓心,100海里為半徑的圓上,船![]() 構(gòu)成正方形編隊(duì)展開搜索,小島
構(gòu)成正方形編隊(duì)展開搜索,小島![]() 在正方形編隊(duì)外(如圖).設(shè)小島
在正方形編隊(duì)外(如圖).設(shè)小島![]() 到
到![]() 的距離為
的距離為![]() ,
,![]() ,
,![]() 船到小島
船到小島![]() 的距離為
的距離為![]() .
.
(1)請分別求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式
的函數(shù)關(guān)系式![]() ,并分別寫出定義域;
,并分別寫出定義域;
(2)當(dāng)![]() 兩艘船之間的距離是多少時(shí)搜救范圍最大(即
兩艘船之間的距離是多少時(shí)搜救范圍最大(即![]() 最大)?
最大)?

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,曲線C的參數(shù)方程為![]() ,(θ為參數(shù)),以原點(diǎn)為極點(diǎn),x軸非負(fù)半軸為極軸建立極坐標(biāo)系.
,(θ為參數(shù)),以原點(diǎn)為極點(diǎn),x軸非負(fù)半軸為極軸建立極坐標(biāo)系.
(1)求曲線C的極坐標(biāo)方程;
(2)在平面直角坐標(biāo)系xOy中,A(﹣2,0),B(0,﹣2),M是曲線C上任意一點(diǎn),求△ABM面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線![]() 的方程為
的方程為![]() ,
,![]() 的方程為
的方程為![]() ,
,![]() 是一條經(jīng)過原點(diǎn)且斜率大于
是一條經(jīng)過原點(diǎn)且斜率大于![]() 的直線.
的直線.
(1)以直角坐標(biāo)系原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸正方向?yàn)闃O軸建立極坐標(biāo)系,求
軸正方向?yàn)闃O軸建立極坐標(biāo)系,求![]() 與
與![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)若![]() 與
與![]() 的一個(gè)公共點(diǎn)
的一個(gè)公共點(diǎn)![]() (異于點(diǎn)
(異于點(diǎn)![]() ),
),![]() 與
與![]() 的一個(gè)公共點(diǎn)為
的一個(gè)公共點(diǎn)為![]() ,當(dāng)
,當(dāng)![]() 時(shí),求
時(shí),求![]() 的直角坐標(biāo)方程.
的直角坐標(biāo)方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某汽車公司最近研發(fā)了一款新能源汽車,并在出廠前對(duì)100輛汽車進(jìn)行了單次最大續(xù)航里程的測試。現(xiàn)對(duì)測試數(shù)據(jù)進(jìn)行分析,得到如圖所示的頻率分布直方圖:

(1)估計(jì)這100輛汽車的單次最大續(xù)航里程的平均值(同一組中的數(shù)據(jù)用該組區(qū)間的中點(diǎn)值代表).
(2)根據(jù)大量的汽車測試數(shù)據(jù),可以認(rèn)為這款汽車的單次最大續(xù)航里程![]() 近似地服從正態(tài)分布
近似地服從正態(tài)分布![]() ,經(jīng)計(jì)算第(1)問中樣本標(biāo)準(zhǔn)差
,經(jīng)計(jì)算第(1)問中樣本標(biāo)準(zhǔn)差![]() 的近似值為50。用樣本平均數(shù)
的近似值為50。用樣本平均數(shù)![]() 作為
作為![]() 的近似值,用樣本標(biāo)準(zhǔn)差
的近似值,用樣本標(biāo)準(zhǔn)差![]() 作為
作為![]() 的估計(jì)值,現(xiàn)任取一輛汽車,求它的單次最大續(xù)航里程恰在250千米到400千米之間的概率.
的估計(jì)值,現(xiàn)任取一輛汽車,求它的單次最大續(xù)航里程恰在250千米到400千米之間的概率.
參考數(shù)據(jù):若隨機(jī)變量服從正態(tài)分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
(3)某汽車銷售公司為推廣此款新能源汽車,現(xiàn)面向意向客戶推出“玩游戲,送大獎(jiǎng)”活動(dòng),客戶可根據(jù)拋擲硬幣的結(jié)果,操控微型遙控車在方格圖上行進(jìn),若遙控車最終停在“勝利大本營”,則可獲得購車優(yōu)惠券3萬元。已知硬幣出現(xiàn)正、反面的概率都是0.5方格圖上標(biāo)有第0格、第1格、第2格、…、第20格。遙控車開始在第0格,客戶每擲一次硬幣,遙控車向前移動(dòng)一次。若擲出正面,遙控車向前移動(dòng)一格(從![]() 到
到![]() )若擲出反面遙控車向前移動(dòng)兩格(從
)若擲出反面遙控車向前移動(dòng)兩格(從![]() 到
到![]() ),直到遙控車移到第19格勝利大本營)或第20格(失敗大本營)時(shí),游戲結(jié)束。設(shè)遙控車移到第
),直到遙控車移到第19格勝利大本營)或第20格(失敗大本營)時(shí),游戲結(jié)束。設(shè)遙控車移到第![]() 格的概率為P試證明
格的概率為P試證明![]() 是等比數(shù)列,并求參與游戲一次的顧客獲得優(yōu)惠券金額的期望值。
是等比數(shù)列,并求參與游戲一次的顧客獲得優(yōu)惠券金額的期望值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)函數(shù)![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程為
處的切線方程為![]() ,求函數(shù)
,求函數(shù)![]() 的解析式;
的解析式;
(2)在(1)的條件下,若![]() 是函數(shù)
是函數(shù)![]() 的零點(diǎn),且
的零點(diǎn),且![]() ,求
,求![]() 的值;
的值;
(3)當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有兩個(gè)零點(diǎn)
有兩個(gè)零點(diǎn)![]() ,且
,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年1月3日嫦娥四號(hào)探測器成功實(shí)現(xiàn)人類歷史上首次月球背面軟著陸,我國航天事業(yè)取得又一重大成就,實(shí)現(xiàn)月球背面軟著陸需要解決的一個(gè)關(guān)鍵技術(shù)問題是地面與探測器的通訊聯(lián)系.為解決這個(gè)問題,發(fā)射了嫦娥四號(hào)中繼星“鵲橋”,鵲橋沿著圍繞地月拉格朗日![]() 點(diǎn)的軌道運(yùn)行.
點(diǎn)的軌道運(yùn)行.![]() 點(diǎn)是平衡點(diǎn),位于地月連線的延長線上.設(shè)地球質(zhì)量為M1,月球質(zhì)量為M2,地月距離為R,
點(diǎn)是平衡點(diǎn),位于地月連線的延長線上.設(shè)地球質(zhì)量為M1,月球質(zhì)量為M2,地月距離為R,![]() 點(diǎn)到月球的距離為r,根據(jù)牛頓運(yùn)動(dòng)定律和萬有引力定律,r滿足方程:
點(diǎn)到月球的距離為r,根據(jù)牛頓運(yùn)動(dòng)定律和萬有引力定律,r滿足方程:
![]() .
.
設(shè)![]() ,由于
,由于![]() 的值很小,因此在近似計(jì)算中
的值很小,因此在近似計(jì)算中![]() ,則r的近似值為
,則r的近似值為
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),
為參數(shù)),![]() 為
為![]() 上的動(dòng)點(diǎn),
上的動(dòng)點(diǎn),![]() 點(diǎn)滿足
點(diǎn)滿足![]() ,點(diǎn)
,點(diǎn)![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)在以為![]() 極點(diǎn),
極點(diǎn),![]() 軸的正半軸為極軸的極坐標(biāo)系中,射線
軸的正半軸為極軸的極坐標(biāo)系中,射線![]() 與
與![]() 的異于極點(diǎn)的交點(diǎn)為
的異于極點(diǎn)的交點(diǎn)為![]() ,與
,與![]() 的異于極點(diǎn)的交點(diǎn)為
的異于極點(diǎn)的交點(diǎn)為![]() ,求
,求![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com