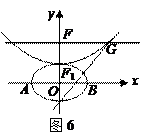已知拋物線
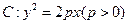
上任意一點到焦點F的距離比到
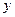
軸的距離大1,(1)求拋物線C的方程;(2)若過焦點F的直線交拋物線于M,N兩點,M在第一象限,且
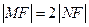
,求直線MN的方程;(3)過點
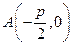
的直線交拋物線
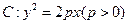
于P、Q兩點,設點P關于
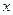
軸的對稱點為R,求證:直線RQ必過定點.
(1)設
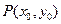
為拋物線
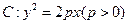
上一點,作

軸,垂足為H,連接PF,因

,所求拋物線C的方程為
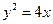
;
(2)由(1)可得焦點坐標為
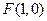
,設
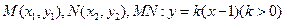
與
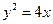
聯(lián)立得,
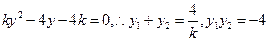
,由
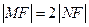
則
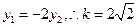
,因此所求的直線方程為
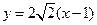
;
(3)因A
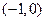
,設
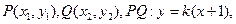
與
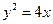
聯(lián)立得
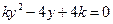
,
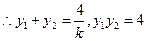
,又因點P關于
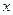
軸的對稱點為R,則
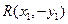
,因此直線RQ的方程為

,即有
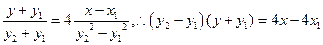
,
因此有
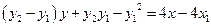
,因
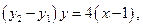
所以直線RQ必過定點

.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
若橢圓經(jīng)過點
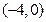
,
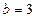
,其焦點在
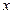
軸上,則該橢圓的標準方程為
。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)



如圖,A為橢圓
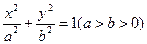
上
的一個動點,弦AB、AC分別過焦點
F
1、F
2。當AC垂直于
x軸時,恰好
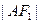
∶
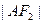
=3∶1.(1)求該橢圓的離心率;
(2)設
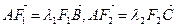
,試判斷
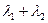
是否為定值?若是,則求出該定值;若不是,請說明理由。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)
設
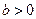
,橢圓方程為
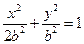
,拋物線方程為
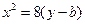
.如圖6所示,過點
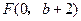
作
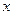
軸的平行線,與拋物線在第一象限的交點為
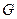
,已知拋物線在點
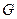
的切線經(jīng)過橢圓的右焦點
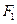
.
(1)求滿足條件的橢圓方程和拋物線方程;
(2)設
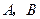
分別是橢圓長軸的左、右端點,試探究在拋物線上是否存在點
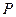
,使得
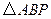
為直角三角形?若存在,請指出共有幾個這樣的點?并說明理由(不必具體求出這些點的坐標).
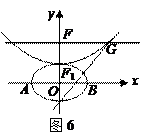
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
橢圓C
1的焦點在x軸上,中心是坐標原點O,且與橢圓
C2:+=1的離心率相同,長軸長是C
2長軸長的一半.A(3,1)為C
2上一點,OA交C
1于P點,P關于x軸的對稱點為Q點,過A作C
2的兩條互相垂直的動弦AB,AC,分別交C
2于B,C兩點,如圖.

(1)求橢圓C
1的標準方程;
(2)求Q點坐標;
(3)求證:B,Q,C三點共線.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
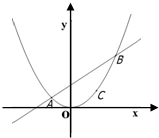
已知過拋物線x
2=4y的焦點,斜率為k(k>0)的直線l交拋物線于A(x
1,y
2),B(x
2,y
2)(x
1<x
2)兩點,且|AB|=8.
(1)求直線l的方程;
(2)若點C(x
3,y
3)是拋物線弧AB上的一點,求△ABC面積的最大值,并求出點C的坐標.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
長度為a的線段AB的兩個端點A、B都在拋物線y2=2px(p>0,a>2p)上滑動,則線段AB的中點M到y(tǒng)軸的最短距離為______.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,已知拋物線y
2=4x的焦點為F.過點P(2,0)的直線交拋物線于A(x
1,y
1),B(x
2,y
2)兩點,直線AF,BF分別與拋物線交于點M,N.
(Ⅰ)求y
1y
2的值;
(Ⅱ)記直線MN的斜率為k
1,直線AB的斜率為k
2.證明:
為定值.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若拋物線
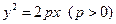
的焦點與雙曲線
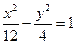
的右焦點重合,則
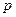
的值為C
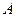
.

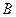
.

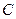
.


.

查看答案和解析>>

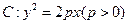 上任意一點到焦點F的距離比到
上任意一點到焦點F的距離比到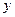 軸的距離大1,(1)求拋物線C的方程;(2)若過焦點F的直線交拋物線于M,N兩點,M在第一象限,且
軸的距離大1,(1)求拋物線C的方程;(2)若過焦點F的直線交拋物線于M,N兩點,M在第一象限,且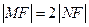 ,求直線MN的方程;(3)過點
,求直線MN的方程;(3)過點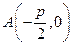 的直線交拋物線
的直線交拋物線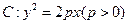 于P、Q兩點,設點P關于
于P、Q兩點,設點P關于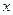 軸的對稱點為R,求證:直線RQ必過定點.
軸的對稱點為R,求證:直線RQ必過定點. 閱讀快車系列答案
閱讀快車系列答案


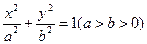 上
上 的一個動點,弦AB、AC分別過焦點
的一個動點,弦AB、AC分別過焦點
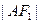 ∶
∶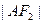 =3∶1.(1)求該橢圓的離心率;
=3∶1.(1)求該橢圓的離心率;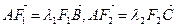 ,試判斷
,試判斷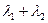 是否為定值?若是,則求出該定值;若不是,請說明理由。
是否為定值?若是,則求出該定值;若不是,請說明理由。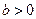 ,橢圓方程為
,橢圓方程為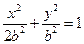 ,拋物線方程為
,拋物線方程為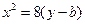 .如圖6所示,過點
.如圖6所示,過點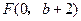 作
作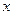 軸的平行線,與拋物線在第一象限的交點為
軸的平行線,與拋物線在第一象限的交點為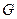 ,已知拋物線在點
,已知拋物線在點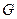 的切線經(jīng)過橢圓的右焦點
的切線經(jīng)過橢圓的右焦點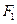 .
.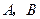 分別是橢圓長軸的左、右端點,試探究在拋物線上是否存在點
分別是橢圓長軸的左、右端點,試探究在拋物線上是否存在點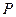 ,使得
,使得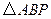 為直角三角形?若存在,請指出共有幾個這樣的點?并說明理由(不必具體求出這些點的坐標).
為直角三角形?若存在,請指出共有幾個這樣的點?并說明理由(不必具體求出這些點的坐標).