
【題目】已知二次函數(shù)![]() 滿足
滿足![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 在
在![]() 上單調(diào),求
上單調(diào),求![]() 的取值范圍;
的取值范圍;
(3)設(shè)![]() (
(![]() 且a≠1),(
且a≠1),(![]() 且
且![]() ),當(dāng)
),當(dāng)![]() 時,
時,![]() 有最大值14,試求a的值.
有最大值14,試求a的值.
【答案】(1)f(x)![]() ;(2)p≤﹣7,或者p≥﹣3;(3)a=3或
;(2)p≤﹣7,或者p≥﹣3;(3)a=3或![]()
【解析】
(1)利用![]() 代入化簡得到答案.
代入化簡得到答案.
(2)化簡得到![]() ,得到對稱軸
,得到對稱軸![]() 或
或![]() 計算得到答案.
計算得到答案.
(3)![]() ,設(shè)
,設(shè)![]() 化簡為二次函數(shù)計算得到答案.
化簡為二次函數(shù)計算得到答案.
(1)∵f(x)=ax2+bx滿足f(x﹣1)=f(x)+x﹣1,
∴a(x﹣1)2+b(x﹣1)=ax2+bx+x﹣1,即ax2﹣(2a﹣b)x+a﹣b=ax2+(b+1)x﹣1,
所以﹣(2a﹣b)=b+1,a﹣b=﹣1,得a![]() ,
,![]() ,
,
所以f(x)![]() .
.
(2)因為g(x)=﹣2f(x)+px=﹣2(![]() )+px=x2+(p﹣1)x,x∈[2,4]上單調(diào),
)+px=x2+(p﹣1)x,x∈[2,4]上單調(diào),
所以其對稱軸x![]() 2,或者
2,或者![]() ,所以p≤﹣7,或者p≥﹣3.
,所以p≤﹣7,或者p≥﹣3.
(3)F(x)=4f(ax)+3a2x﹣1=a2x+2ax﹣1,(a>0且a≠1),
當(dāng)x∈[﹣1,1]時,令t=ax,y=t2+2t﹣1=(t+1)2﹣2,
當(dāng)a>1時,t![]() ,ymax=F(a)=(a+1)2﹣2=14,得a=3;
,ymax=F(a)=(a+1)2﹣2=14,得a=3;
當(dāng)0<a<1時,t![]() ,
,![]() ,得a
,得a![]() .
.
故a=3或![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標原點為極點,
為參數(shù)),以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求![]() 和
和![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若曲線![]() 截直線
截直線![]() 所得線段的中點坐標為
所得線段的中點坐標為![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是定義在R上的奇函數(shù),且滿足
是定義在R上的奇函數(shù),且滿足![]() ,
,![]() =1,數(shù)列{
=1,數(shù)列{![]() }滿足
}滿足![]() =﹣1,
=﹣1, ![]() (
(![]() ),其中
),其中![]() 是數(shù)列{
是數(shù)列{![]() }的前n項和,則
}的前n項和,則![]() =
=
A. ﹣2 B. ﹣1 C. 0 D. 1
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)![]() 同時滿足:①對于定義域上的任意
同時滿足:①對于定義域上的任意![]() ,恒有
,恒有![]() ;②對于定義域上的任意
;②對于定義域上的任意![]() ,當(dāng)
,當(dāng)![]() 時,恒有
時,恒有![]() ,則稱函數(shù)
,則稱函數(shù)![]() 為“理想函數(shù)”.給出下列四個函數(shù)中:①
為“理想函數(shù)”.給出下列四個函數(shù)中:① ![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④ 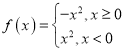 ,能被稱為“理想函數(shù)”的有_____(請將所有正確命題的序號都填上).
,能被稱為“理想函數(shù)”的有_____(請將所有正確命題的序號都填上).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a是實常數(shù),函數(shù)![]() .
.
(1)若曲線![]() 在
在![]() 處的切線過點A(0,﹣2),求實數(shù)a的值;
處的切線過點A(0,﹣2),求實數(shù)a的值;
(2)若![]() 有兩個極值點
有兩個極值點![]() (
(![]() ),
),
①求證:![]() ;
;
②求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了適應(yīng)高考改革,某中學(xué)推行“創(chuàng)新課堂”教學(xué).高一平行甲班采用“傳統(tǒng)教學(xué)”的教學(xué)方式授課,高一平行乙班采用“創(chuàng)新課堂”的教學(xué)方式授課,為了比較教學(xué)效果,期中考試后,分別從兩個班中各隨機抽取![]() 名學(xué)生的成績進行統(tǒng)計分析,結(jié)果如下表:(記成績不低于
名學(xué)生的成績進行統(tǒng)計分析,結(jié)果如下表:(記成績不低于![]() 分者為“成績優(yōu)秀”)
分者為“成績優(yōu)秀”)
分數(shù) |
|
|
|
|
|
|
|
甲班頻數(shù) |
|
|
|
|
|
|
|
乙班頻數(shù) |
|
|
|
|
|
|
|
(1)由以上統(tǒng)計數(shù)據(jù)填寫下面的![]() 列聯(lián)表,并判斷是否有
列聯(lián)表,并判斷是否有![]() 以上的把握認為“成績優(yōu)秀與教學(xué)方式有關(guān)”?
以上的把握認為“成績優(yōu)秀與教學(xué)方式有關(guān)”?
甲班 | 乙班 | 總計 | |
成績優(yōu)秀 | |||
成績不優(yōu)秀 | |||
總計 |
(2)在上述樣本中,學(xué)校從成績?yōu)?/span>![]() 的學(xué)生中隨機抽取
的學(xué)生中隨機抽取![]() 人進行學(xué)習(xí)交流,求這
人進行學(xué)習(xí)交流,求這![]() 人來自同一個班級的概率.
人來自同一個班級的概率.
參考公式:![]() ,其中
,其中![]() .
.
臨界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]() 滿足條件
滿足條件![]() 是偶函數(shù),
是偶函數(shù), ![]() ,且
,且![]() 的圖象與直線
的圖象與直線![]() 恰有一個公共點.
恰有一個公共點.
(1)求![]() 的解析式;
的解析式;
(2)設(shè)![]() ,是否存在實數(shù)
,是否存在實數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值為2?如果存在,求出
上的最大值為2?如果存在,求出![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)當(dāng)![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處切線的方程;
處切線的方程;
(Ⅱ)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)當(dāng)![]() 時,
時,![]() 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某工廠生產(chǎn)一種產(chǎn)品,根據(jù)預(yù)測可知,該產(chǎn)品的產(chǎn)量平穩(wěn)增長,記2015年為第1年,第x年與年產(chǎn)量![]() (萬件)之間的關(guān)系如下表所示:
(萬件)之間的關(guān)系如下表所示:
x | 1 | 2 | 3 | 4 |
| 4.00 | 5.52 | 7.00 | 8.49 |
現(xiàn)有三種函數(shù)模型:![]() ,
,![]() ,
,![]()
(1)找出你認為最適合的函數(shù)模型,并說明理由,然后選取![]() 這兩年的數(shù)據(jù)求出相應(yīng)的函數(shù)解析式;
這兩年的數(shù)據(jù)求出相應(yīng)的函數(shù)解析式;
(2)因受市場環(huán)境的影響,2020年的年產(chǎn)量估計要比預(yù)計減少30%,試根據(jù)所建立的函數(shù)模型,估計2020年的年產(chǎn)量.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com