
【題目】已知函數(shù)![]() (
(![]() ,
,![]() )的圖象的相鄰兩條對稱軸之間的距離為4,且有一個零點(diǎn)為
)的圖象的相鄰兩條對稱軸之間的距離為4,且有一個零點(diǎn)為![]() .
.
(1)求函數(shù)![]() 的解析式;
的解析式;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若![]() 在
在![]() 上恒成立,求實(shí)數(shù)
上恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據(jù)題意,由周期和零點(diǎn),求得函數(shù)對應(yīng)的參數(shù)即可;
(2)由![]() 求得
求得![]() ,湊角,利用正弦和角公式計(jì)算即可;
,湊角,利用正弦和角公式計(jì)算即可;
(3)將恒成立問題轉(zhuǎn)化為最值問題,再求三角函數(shù)的最值即可.
(1)因?yàn)楹瘮?shù)![]() 圖象的相鄰兩條對稱軸之間的距離為4,
圖象的相鄰兩條對稱軸之間的距離為4,
所以函數(shù)![]() 的最小正周期是8.
的最小正周期是8.
所以![]() ,解得
,解得![]() .
.
所以![]() .
.
因?yàn)楹瘮?shù)![]() 有一個零點(diǎn)
有一個零點(diǎn)![]() ,
,
所以![]() ,
,
得![]() (
(![]() ).
).
解得![]() (
(![]() ).
).
由![]() 知,
知,![]() ,
,
所以![]() ;
;
(2)由![]() ,得
,得![]() ,
,
即![]() ,
,
由![]() ,得
,得![]() ,
,
所以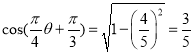 .
.
所以![]()
![]()
![]()
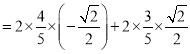
![]()
(3)由![]() ,得
,得![]() ,
,
所以當(dāng)![]() 時,
時,![]() ,
,
若![]() 在
在![]() 上恒成立,
上恒成立,
則![]() 在
在![]() 上恒成立,
上恒成立,
則![]() ,即
,即![]() ,
,
解得![]() .
.
故![]() 的取值范圍為
的取值范圍為![]() .
.


 互動英語系列答案
互動英語系列答案 名牌學(xué)校分層周周測系列答案
名牌學(xué)校分層周周測系列答案 黃岡海淀全程培優(yōu)測試卷系列答案
黃岡海淀全程培優(yōu)測試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知某觀光海域AB段的長度為3百公里,一超級快艇在AB段航行,經(jīng)過多次試驗(yàn)得到其每小時航行費(fèi)用Q(單位:萬元)與速度v(單位:百公里/小時)(0≤v≤3)的以下數(shù)據(jù):
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
為描述該超級快艇每小時航行費(fèi)用Q與速度v的關(guān)系,現(xiàn)有以下三種函數(shù)模型供選擇:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)試從中確定最符合實(shí)際的函數(shù)模型,并求出相應(yīng)的函數(shù)解析式;
(2)該超級快艇應(yīng)以多大速度航行才能使AB段的航行費(fèi)用最少?并求出最少航行費(fèi)用.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是定義在
是定義在![]() 上的奇函數(shù),且滿足
上的奇函數(shù),且滿足![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ,則函數(shù)
,則函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上所有零點(diǎn)的個數(shù)為( )
上所有零點(diǎn)的個數(shù)為( )
A.0B.2C.4D.6
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】新能源汽車包括純電動汽車、增程式電動汽車、混合動力汽車、燃料電池電動汽車、氫發(fā)動機(jī)汽車、其他新能源汽車等.它是未來汽車的發(fā)展方向.一個新能源汽車制造廠引進(jìn)了一條新能源汽車整車裝配流水線,這條流水線生產(chǎn)的新能源汽車數(shù)量![]() (輛)與創(chuàng)造的價值
(輛)與創(chuàng)造的價值![]() (萬元)之間滿足二次函數(shù)關(guān)系.已知產(chǎn)量為0時,創(chuàng)造的價值也為0;當(dāng)產(chǎn)量為40000輛時,創(chuàng)造的價值達(dá)到最大6000萬元.若這家工廠希望利用這條流水線創(chuàng)收達(dá)到5625萬元,則它可能生產(chǎn)的新能源汽車數(shù)量是___________輛.
(萬元)之間滿足二次函數(shù)關(guān)系.已知產(chǎn)量為0時,創(chuàng)造的價值也為0;當(dāng)產(chǎn)量為40000輛時,創(chuàng)造的價值達(dá)到最大6000萬元.若這家工廠希望利用這條流水線創(chuàng)收達(dá)到5625萬元,則它可能生產(chǎn)的新能源汽車數(shù)量是___________輛.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】生活中萬事萬物都是有關(guān)聯(lián)的,所有直線中有關(guān)聯(lián)直線,所有點(diǎn)中也有相關(guān)點(diǎn),現(xiàn)在定義:平面內(nèi)如果兩點(diǎn)![]() 、
、![]() 都在函數(shù)
都在函數(shù)![]() 的圖像上,而且滿足
的圖像上,而且滿足![]() 、
、![]() 兩點(diǎn)關(guān)于原點(diǎn)對稱,則稱點(diǎn)對(
兩點(diǎn)關(guān)于原點(diǎn)對稱,則稱點(diǎn)對(![]() 、
、![]() )是函數(shù)
)是函數(shù)![]() 的“相關(guān)對稱點(diǎn)對”(注明:點(diǎn)對(
的“相關(guān)對稱點(diǎn)對”(注明:點(diǎn)對(![]() 、
、![]() )與(
)與(![]() 、
、![]() )看成同一個“相關(guān)對稱點(diǎn)對”).已知函數(shù)
)看成同一個“相關(guān)對稱點(diǎn)對”).已知函數(shù)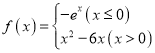 ,則這個函數(shù)的“相關(guān)對稱點(diǎn)對”有( )
,則這個函數(shù)的“相關(guān)對稱點(diǎn)對”有( )
A.0個B.1個C.2個D.3個
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,且
,且![]() 上的最大值為
上的最大值為![]() .
.
![]() 求函數(shù)
求函數(shù)![]() 的解析式;
的解析式;
![]() 判斷
判斷![]() 在
在![]() 內(nèi)的零點(diǎn)的個數(shù),并加以證明.
內(nèi)的零點(diǎn)的個數(shù),并加以證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若![]() ,求證:函數(shù)
,求證:函數(shù)![]() 恰有一個負(fù)零點(diǎn);(用圖象法證明不給分)
恰有一個負(fù)零點(diǎn);(用圖象法證明不給分)
(2)若函數(shù)![]() 恰有三個零點(diǎn),求實(shí)數(shù)
恰有三個零點(diǎn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
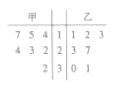
【題目】某賽季,甲、乙兩名籃球運(yùn)動員都參加了7場比賽,他們所有比賽得分的情況用如圖所示的莖葉圖表示.
(1)求甲、乙兩名運(yùn)動員得分的中位數(shù);
(2)你認(rèn)為哪位運(yùn)動員的成績更穩(wěn)定?
(3)如果從甲、乙兩位運(yùn)動員的7場得分中各隨機(jī)抽取一場的得分,求甲的得分大于乙的得分的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com