（本題滿分10分）已知函數
是奇函數:
（1）求實數
和
的值； （2）證明
在區間
上的單調遞減
（3）已知
且不等式
對任意的
恒成立，求實數
的取值范圍．
優等生題庫系列答案
53天天練系列答案科目：高中數學 來源： 題型：解答題
（本題滿分14分，第1小題6分，第2小題8分）
已知函數
，其中常數a > 0．
(1) 當a = 4時，證明函數f(x)在
上是減函數；
(2) 求函數f(x)的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分12分）
定義在
上的函數
，對于任意的實數
，恒有
，且當
時，
。
（1）求
及
的值域。
（2）判斷在上的單調性，并證明。
（3）設
，
，
,求
的范圍。
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（12分）已知函數
為奇函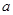數，
為常數，
（1）求實數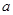的值；
（2）證明：函數
在區間
上單調遞增；
（3）若對于區間
上的每一個
值，不等式
恒成立，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
本題12分）
已知函數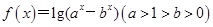
.
(1)求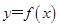
的定義域；
(2)在函數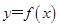的圖象上是否存在不同的兩點，使得過這兩點的直線平行于x軸；
(3)當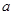
，b滿足什么條件時，
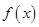在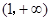
上恒取正值.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
海事救援船對一艘失事船進行定位：以失事船的當前位置為原點，以正北方向為
軸正方向建立平面直角坐標系（以1海里為單位長度），則救援船恰好在失事船正南方向12海里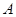
處，如圖，現假設：①失事船的移動路徑可視為拋物線
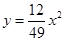；②定位后救援船即刻沿直線勻速前往救援；③救援船出發
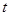小時后，失事船所在位置的橫坐標為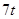
（1）當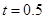
時，寫出失事船所在位置
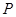的縱坐標，若此時兩船恰好會合，求救援船速度的大小和方向 (若確定方向時涉及到的角為非特殊角，用符號及其滿足的條件表示即可)
（2）問救援船的時速至少是多少海里才能追上失事船？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知定義在（－∞，—1）∪（1，+∞）上的奇函數滿足：①f(3)=1;②對任意的x>2, 均有f(x)>0,③對任意的x>0,y>0.均有f(x+1)+f(y+1)=f(xy+1)
⑴試求f(2)的值;
⑵證明f(x)在(1,+∞)上單調遞增；
⑶是否存在實數a,使得f(cos2θ+asinθ)<3對任意的θ
（0，π）恒成立？若存在，請求出a的范圍；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分12分）
已知函數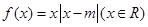
，且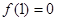
.
（Ⅰ）求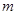
的值，并用分段函數的形式來表示
；
（Ⅱ）在如圖給定的直角坐標系內作出函數的草圖；
（III）由圖象寫出函數的奇偶性及單調區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
；（2）
。
，
即
所以
且不等式
恒成立，求實數
的取值范圍． 
為奇函數得：
，
，且
在區間
上的單調遞減，
任意的
（a＞0，a≠1）．