
【題目】已知正實(shí)數(shù)列a1,a2,…滿足對于每個(gè)正整數(shù)k,均有![]() ,證明:
,證明:
(Ⅰ)a1+a2≥2;
(Ⅱ)對于每個(gè)正整數(shù)n≥2,均有a1+a2+…+an≥n.
【答案】(Ⅰ)見解析(Ⅱ)見解析
【解析】
(Ⅰ)利用已知條件可得![]() ,然后結(jié)合基本不等式可證;
,然后結(jié)合基本不等式可證;
(Ⅱ)利用數(shù)學(xué)歸納法進(jìn)行證明.
證明:(Ⅰ)當(dāng)k=1時(shí),有![]() ,即,
,即,![]() ,
,
∵![]() ,數(shù)列為正實(shí)數(shù)列,
,數(shù)列為正實(shí)數(shù)列,
由基本不等式1![]() ,∴
,∴![]() ,
,
∴a1+a2≥2.
(Ⅱ)用數(shù)學(xué)歸納法:
由(Ⅰ)得n=2時(shí),a1+a2≥2,不等式成立;
假設(shè)當(dāng)n=k(k≥2)時(shí),a1+a2+…+ak≥k成立;
則當(dāng)n=k+1時(shí),a1+a2+…+ak+ak+1≥k![]() ,
,
要證k![]() k+1,即證
k+1,即證![]() 1,
1,
即為kak≥ak2+k﹣1,即為(ak﹣1)(k﹣1)≥0,
∵k≥2,∴k﹣1≥1,當(dāng)ak﹣1≥0時(shí),a1+a2+…+ak+ak+1≥k+1,
∴對于每個(gè)正整數(shù)n≥2,均有a1+a2+…+an≥n.
當(dāng)0<ak<1時(shí),
∵對于每個(gè)正整數(shù)k,均有![]() ,
,
∴![]() ,則
,則![]() ,
,

a1+a2+…+an+an+1![]() an+1
an+1![]() n﹣1+2=n+1.
n﹣1+2=n+1.
綜上,對于每個(gè)正整數(shù)n≥2,均有a1+a2+…+an≥n.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優(yōu)秀生快樂假期每一天全新寒假作業(yè)本系列答案
優(yōu)秀生快樂假期每一天全新寒假作業(yè)本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,(其中
,(其中![]() 是自然對數(shù)的底數(shù)).
是自然對數(shù)的底數(shù)).
(1)若![]() ,求函數(shù)
,求函數(shù)![]() 在
在![]() 上的最大值.
上的最大值.
(2)若![]() ,關(guān)于x的方程
,關(guān)于x的方程![]() 有且僅有一個(gè)根,求實(shí)數(shù)k的取值范圍.
有且僅有一個(gè)根,求實(shí)數(shù)k的取值范圍.
(3)若對任意的![]() 、
、![]() ,
,![]() ,不等式
,不等式![]() 都成立,求實(shí)數(shù)a的取值范圍.
都成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】矩形ABCD中,![]() ,沿對角線AC將三角形ADC折起,得到四面體
,沿對角線AC將三角形ADC折起,得到四面體![]() ,四面體
,四面體![]() 外接球表面積為
外接球表面積為![]() ,當(dāng)四面體
,當(dāng)四面體![]() 的體積取最大值時(shí),四面體
的體積取最大值時(shí),四面體![]() 的表面積為( )
的表面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《中國詩詞大會(huì)》是央視推出的一檔以“賞中華詩詞,尋文化基因,品生活之美”為宗旨的大型文化類競賽節(jié)目,邀請全國各個(gè)年齡段、各個(gè)領(lǐng)域的詩詞愛好者共同參與詩詞知識比拼。“百人團(tuán)”由一百多位來自全國各地的選手組成,成員上至古稀老人,下至垂髫小兒,人數(shù)按照年齡分組統(tǒng)計(jì)如下表:
分組(年齡) |
|
|
|
頻數(shù)(人) |
|
|
|
(1)用分層抽樣的方法從“百人團(tuán)”中抽取![]() 人參加挑戰(zhàn),求從這三個(gè)不同年齡組中分別抽取的挑戰(zhàn)者的人數(shù);
人參加挑戰(zhàn),求從這三個(gè)不同年齡組中分別抽取的挑戰(zhàn)者的人數(shù);
(2)在(1)中抽出的![]() 人中,任選
人中,任選![]() 人參加一對一的對抗比賽,求這
人參加一對一的對抗比賽,求這![]() 人來自同一年齡組的概率。
人來自同一年齡組的概率。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是橢圓
是橢圓![]() 的左、右頂點(diǎn),
的左、右頂點(diǎn),![]() 為橢圓
為橢圓![]() 的左、右焦點(diǎn),點(diǎn)
的左、右焦點(diǎn),點(diǎn)![]() 為橢圓
為橢圓![]() 上一點(diǎn)(
上一點(diǎn)(![]() 點(diǎn)在第一象限),線段
點(diǎn)在第一象限),線段![]() 與圓
與圓![]() 相切于點(diǎn)
相切于點(diǎn)![]() ,且點(diǎn)
,且點(diǎn)![]() 為線段
為線段![]() 的中點(diǎn).
的中點(diǎn).
(1)求線段![]() 的長;
的長;
(2)求橢圓![]() 的離心率;
的離心率;
(3)設(shè)直線![]() 交橢圓于
交橢圓于![]() 兩點(diǎn)(其中點(diǎn)
兩點(diǎn)(其中點(diǎn)![]() 在第一象限),過點(diǎn)
在第一象限),過點(diǎn)![]() 作
作![]() 的平行線
的平行線![]() 交橢圓
交橢圓![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
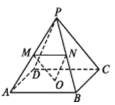
【題目】如圖,在棱長均相等的四棱錐![]() 中,
中, ![]() 為底面正方形的中心,
為底面正方形的中心, ![]() ,
,![]() 分別為側(cè)棱
分別為側(cè)棱![]() ,
,![]() 的中點(diǎn),有下列結(jié)論正確的有:( )
的中點(diǎn),有下列結(jié)論正確的有:( )
A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() ∥平面
∥平面![]()
C.直線![]() 與直線
與直線![]() 所成角的大小為
所成角的大小為![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 過點(diǎn)
過點(diǎn)![]() ,其參數(shù)方程為
,其參數(shù)方程為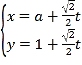 (
(![]() 為參數(shù),
為參數(shù),![]() ).以
).以![]() 為極點(diǎn),
為極點(diǎn),![]() 軸非負(fù)半軸為極軸,建立極坐標(biāo)系,曲線
軸非負(fù)半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)已知曲線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點(diǎn),且
兩點(diǎn),且![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,E為AB的中點(diǎn).將
,E為AB的中點(diǎn).將![]() 沿CE折起,使點(diǎn)B到達(dá)點(diǎn)F的位置,且平面CEF與平面ADCE所成的二面角為
沿CE折起,使點(diǎn)B到達(dá)點(diǎn)F的位置,且平面CEF與平面ADCE所成的二面角為![]() .
.
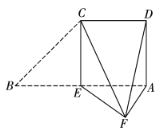
(1)求證:平面![]() 平面AEF;
平面AEF;
(2)求直線DF與平面CEF所成角的正弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com