
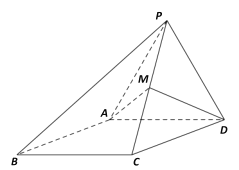
【題目】如圖,四棱錐![]() ,側面
,側面![]() 是邊長為2的正三角形,且與底面垂直,底面
是邊長為2的正三角形,且與底面垂直,底面![]() 是
是![]() 的菱形,
的菱形, ![]() 為棱
為棱![]() 上的動點,且
上的動點,且![]() .
.
(I)求證: ![]() 為直角三角形;
為直角三角形;
(II)試確定![]() 的值,使得二面角
的值,使得二面角![]() 的平面角余弦值為
的平面角余弦值為![]() .
.
【答案】(1)見解析;(II) ![]() .
.
【解析】試題分析:(1)取![]() 中點
中點![]() ,連結
,連結![]() ,以
,以![]() 為原點,
為原點, ![]() 為
為![]() 軸,
軸, ![]() 為
為![]() 軸,
軸, ![]() 為
為![]() 軸,建立空間直角坐標系,利用向量法能證明
軸,建立空間直角坐標系,利用向量法能證明![]() 為直角三角形;(2)設
為直角三角形;(2)設![]() ,由
,由![]() ,得
,得![]() ,求出平面
,求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,,根據空間向量夾角余弦公式能求出結果.
的法向量,,根據空間向量夾角余弦公式能求出結果.
試題解析:(I)取![]() 中點
中點![]() ,連結
,連結![]() ,依題意可知
,依題意可知![]() 均為正三角形,所以
均為正三角形,所以![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
因為![]() ,所以
,所以![]() ,即
,即![]() ,
,
從而![]() 為直角三角形.
為直角三角形.
說明:利用 ![]() 平面
平面![]() 證明正確,同樣滿分!
證明正確,同樣滿分!
(II)[向量法]由(I)可知![]() ,又平面
,又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
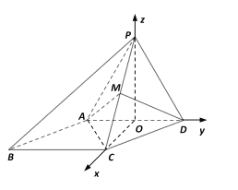
以![]() 為原點,建立空間直角坐標系
為原點,建立空間直角坐標系![]() 如圖所示,則
如圖所示,則
![]() ,
,![]()
由![]() 可得點
可得點![]() 的坐標
的坐標![]()
所以![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,則
,則![]() ,
,
即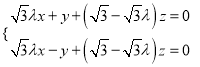 解得
解得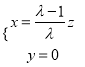 ,
,
令![]() ,得
,得![]() ,
,
顯然平面![]() 的一個法向量為
的一個法向量為![]() ,
,
依題意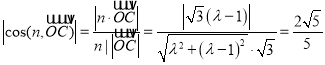 ,
,
解得![]() 或
或![]() (舍去),
(舍去),
所以,當![]() 時,二面角
時,二面角![]() 的余弦值為
的余弦值為![]() .
.
[傳統法]由(I)可知![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() 為二面角
為二面角![]() 的平面角,
的平面角,
即![]() ,
,
在![]() 中,
中, ![]() ,
,
所以![]()
![]() ,
,
由正弦定理可得![]() ,即
,即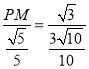
解得![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以,當![]() 時,二面角
時,二面角![]() 的余弦值為
的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】對某校高一年級學生參加社區服務次數進行統計,隨機抽取![]() 名學生作為樣本,得到這
名學生作為樣本,得到這![]() 名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖如下:
名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖如下:
分組 | 頻數 | 頻率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合計 |
| 1 |

(1)求出表中![]() 及圖中
及圖中![]() 的值;
的值;
(2)試估計他們參加社區服務的平均次數;
(3)在所取樣本中,從參加社區服務的次數不少于20次的學生中任選2人,求至少1人參加社區服務次數在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
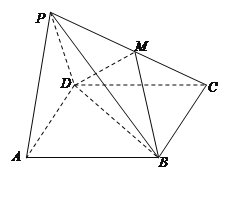
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是邊長為
是邊長為![]() 的等邊三角形,
的等邊三角形, ![]() ,
, ![]() 在
在![]() 上,且
上,且![]() ∥面BDM.
∥面BDM.
(1)求直線PC與平面BDM所成角的正弦值;
(2)求平面BDM與平面PAD所成銳二面角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
: ![]() (
(![]() ),設
),設![]() 為圓
為圓![]() 與
與![]() 軸負半軸的交點,過點
軸負半軸的交點,過點![]() 作圓
作圓![]() 的弦
的弦![]() ,并使弦
,并使弦![]() 的中點恰好落在
的中點恰好落在![]() 軸上.
軸上.
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)延長![]() 交曲線
交曲線![]() 于點
于點![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 交于點
交于點![]() ,試判斷以點
,試判斷以點![]() 為圓心,線段
為圓心,線段![]() 長為半徑的圓與直線
長為半徑的圓與直線![]() 的位置關系,并證明你的結論.
的位置關系,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
, ![]() ),曲線
),曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .
.
(Ⅰ)求![]() ,
, ![]() 的值;
的值;
(Ⅱ)證明: ![]() ;
;
(Ⅲ)已知滿足![]() 的常數為
的常數為![]() .令函數
.令函數![]() (其中
(其中![]() 是自然對數的底數,
是自然對數的底數, ![]() ),若
),若![]() 是
是![]() 的極值點,且
的極值點,且![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三年級一次數學考試后,為了解學生的數學學習情況,隨機抽取![]() 名學生的數學成績,制成表所示的頻率分布表.
名學生的數學成績,制成表所示的頻率分布表.
組號 | 分組 | 頻數 | 頻率 |
第一組 |
|
|
|
第二組 |
|
|
|
第三組 |
|
|
|
第四組 |
|
|
|
第五組 |
|
|
|
合計 |
|
| |
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)若從第三、四、五組中用分層抽樣方法抽取![]() 名學生,并在這
名學生,并在這![]() 名學生中隨機抽取
名學生中隨機抽取![]() 名學生與張老師面談,求第三組中至少有
名學生與張老師面談,求第三組中至少有![]() 名學生與張老師面談的概率
名學生與張老師面談的概率
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在研究塞卡病毒(Zika virus)某種疫苗的過程中,為了研究小白鼠連續接種該種疫苗后出現![]() 癥狀的情況,做接種試驗,試驗設計每天接種一次,連續接種3天為一個接種周期.已知小白鼠接種后當天出現
癥狀的情況,做接種試驗,試驗設計每天接種一次,連續接種3天為一個接種周期.已知小白鼠接種后當天出現![]() 癥狀的概率為
癥狀的概率為![]() ,假設每次接種后當天是否出現
,假設每次接種后當天是否出現![]() 癥狀與上次接種無關.
癥狀與上次接種無關.
(1)若出現![]() 癥狀即停止試驗,求試驗至多持續一個接種周期的概率;
癥狀即停止試驗,求試驗至多持續一個接種周期的概率;
(2)若在一個接種周期內出現3次![]() 癥狀,則這個接種周期結束后終止試驗,試驗至多持續3個周期,設接種試驗持續的接種周期數為
癥狀,則這個接種周期結束后終止試驗,試驗至多持續3個周期,設接種試驗持續的接種周期數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com