
設(shè)函數(shù)![]() .
.
(Ⅰ)若x=時,![]() 取得極值,求
取得極值,求![]() 的值;
的值;
(Ⅱ)若![]() 在其定義域內(nèi)為增函數(shù),求
在其定義域內(nèi)為增函數(shù),求![]() 的取值范圍;
的取值范圍;
(Ⅲ)設(shè)![]() ,當
,當![]() =-1時,證明
=-1時,證明![]() 在其定義域內(nèi)恒成立,并證明
在其定義域內(nèi)恒成立,并證明![]() (
(![]() ).
).
(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 的取值范圍是
的取值范圍是![]() (Ⅲ)見解析
(Ⅲ)見解析
![]() ,
,
(Ⅰ)因為![]() 時,
時,![]() 取得極值,所以
取得極值,所以![]() ,
,
即![]() 故
故![]() . ………………………………………………3分
. ………………………………………………3分
(Ⅱ)![]() 的定義域為
的定義域為![]() .
.
方程![]() 的判別式
的判別式![]() ,
,
(1) 當![]() , 即
, 即![]() 時,
時,![]() ,
,
![]() 在
在![]() 內(nèi)恒成立, 此時
內(nèi)恒成立, 此時![]() 為增函數(shù).
為增函數(shù).
(2) 當![]() , 即
, 即![]() 或
或![]() 時,
時,
要使![]() 在定義域
在定義域![]() 內(nèi)為增函數(shù),
內(nèi)為增函數(shù),
只需在![]() 內(nèi)有
內(nèi)有![]() 即可,
即可,
設(shè)![]() ,
,
由 得
得 ![]() , 所以
, 所以![]() .
.
由(1) (2)可知,若![]() 在其定義域內(nèi)為增函數(shù),
在其定義域內(nèi)為增函數(shù),![]() 的取值范圍是
的取值范圍是![]() .
.
………………………………………………9分
(Ⅲ)證明:![]() ,當
,當![]() =-1時,
=-1時,![]() ,其定義域是
,其定義域是![]() ,
,
令![]() ,得
,得![]() .則
.則![]() 在
在![]() 處取得極大值,也是最大值.
處取得極大值,也是最大值.
而![]() .所以
.所以![]() 在
在![]() 上恒成立.因此
上恒成立.因此![]() .
.
因為![]() ,所以
,所以![]() .則
.則![]() .
.
所以![]()
=![]()
<![]()
=![]() =
=![]() .
.
所以結(jié)論成立.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源: 題型:
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| 1 |
| 2 |
| x+1 |
| x-1 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| 2x+1-n |
| x2+x+1 |
| lim |
| n→∞ |
| ||
| Cn |
| 1 |
| C1 |
| 1 |
| C2 |
| 1 |
| Cn |
| m |
| 25 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(08年西工大附中文)設(shè)函數(shù)![]() ,其中
,其中![]()
(Ⅰ)若f(x)在x=3處取得極值,求常數(shù)a 的值;
(Ⅱ)若f(x)在![]() 上為增函數(shù),求a的取值范圍
上為增函數(shù),求a的取值范圍
查看答案和解析>>
科目:高中數(shù)學 來源:2012年河南省普通高中畢業(yè)班高考適應性測試數(shù)學試卷(理科)(解析版) 題型:解答題
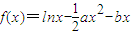 .
.查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com