
【題目】已知四棱錐P-ABCD的體積為 ![]() ,其三視圖如圖所示,其中正視圖為等腰 三角形,側視圖為直角三角形,俯視圖是直角梯形.
,其三視圖如圖所示,其中正視圖為等腰 三角形,側視圖為直角三角形,俯視圖是直角梯形.
(1)求正視圖的面積;
(2)求四棱錐P-ABCD的側面積.
【答案】
(1)解:如圖所示四棱錐P-ABCD的高為PA,底面積為S= ![]() ·CD=
·CD= ![]() ×1=
×1= ![]()
∴四棱錐P-ABCD的體積V四棱錐P-ABCD= ![]() S·PA=
S·PA= ![]() ×
× ![]() ·PA=
·PA= ![]() ,∴PA=
,∴PA= ![]()
∴正視圖的面積為S= ![]() ×2×
×2× ![]() =
= ![]() .
.
(2)解:如圖所示,過A作AE∥CD交BC于E,連接PE.根據三視圖可知,E是BC的中點,
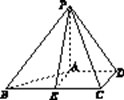
且BE=CE=1,AE=CD=1,且BC⊥AE,AB= ![]()
又PA⊥平面ABCD,∴PA⊥BC,PA⊥DC,PD= ![]() ,∴BC⊥面PAE,∴BC⊥PE,
,∴BC⊥面PAE,∴BC⊥PE,
又DC⊥AD,∴DC⊥面PAD,∴DC⊥PD,且PA⊥平面ABCD.∴PA⊥AE,
∴PE2=PA2+AE2=3.∴PE= ![]() .
.
∴四棱錐P-ABCD的側面積為
S=S△PAB+ S△PAD+ S△PCD+ S△PBC= ![]() ·
· ![]() ·
· ![]() +
+ ![]() ·
· ![]() ·1+
·1+ ![]() ·1·
·1· ![]() +
+ ![]() ·2·
·2· ![]() =
= ![]() .
.
【解析】(I)由三視圖還原直觀圖,關鍵是放在長方體中,根據三視圖得到直觀圖,及長度大小,可得;
(II)根據棱錐的體積公式V=![]() 可得。
可得。
【考點精析】解答此題的關鍵在于理解由三視圖求面積、體積的相關知識,掌握求體積的關鍵是求出底面積和高;求全面積的關鍵是求出各個側面的面積,以及對由三視圖還原實物圖的理解,了解正視圖:從前往后;側視圖:從左往右;俯視圖:從上往下.


科目:高中數學 來源: 題型:
【題目】設命題p:方程x2+2mx+1=0有兩個不相等的負根,命題q:x∈R,x2+2(m﹣2)x﹣3m+10≥0恒成立.
(1)若命題p、q均為真命題,求m的取值范圍;
(2)若命題p∧q為假,命題p∨q為真,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設OABC是四面體,G1是△ABC的重心,G是OG1上一點,且OG=3GG1 , 若 ![]() =x
=x ![]() +y
+y ![]() +z
+z ![]() ,則(x,y,z)為( )
,則(x,y,z)為( )
A.( ![]() ,
, ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐 ![]() 中,底面ABCD是菱 形,PA=PB,且側面PAB⊥平面ABCD,點E是AB的中點.
中,底面ABCD是菱 形,PA=PB,且側面PAB⊥平面ABCD,點E是AB的中點.
(1)求證:PE⊥AD;
(2)若CA=CB,求證:平面PEC⊥平面PAB.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 且a1=1,當n≥2時,Sn=2an .
(1)求證數列{an}為等比數列,并求出an的通項公式;
(2)設若bn=an+1﹣1,設數列{anbn}的前n項和為Tn , 求Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合A={x|x2﹣3x+2=0},B={x|x2+2(a+1)x+(a2﹣5)=0}.
(1)若A∩B={2},求實數a的值;
(2)若A∪B=A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的偶函數,且當x≤0時,f(x)=x2+2x.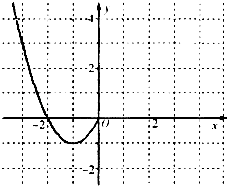
(1)現已畫出函數f(x)在y軸左側的圖象,如圖所示,請補出完整函數f(x)的圖象,并根據圖象寫出函數f(x)的增區間;
(2)寫出函數f(x)的解析式和值域;
(3)若方程f(x)﹣m=0有四個解,求m的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥側面A1ABB1 , 且AA1=AB=2 
(1)求證:AB⊥BC;
(2)若AC=2 ![]() ,求銳二面角A﹣A1C﹣B的大小.
,求銳二面角A﹣A1C﹣B的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com