
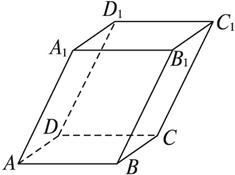
(1)求AC1的長;
(2)求AC1與面ABCD所成的角.
解:(向量法)記a=![]() ,b=
,b=![]() ,c=
,c=![]() ,
,
于是|a|=|b|=|c|=1,〈a,b〉=〈b,c〉=〈c,a〉=60°.
(1)![]()
∴![]() =
=![]() =a2+b2+c2+2a·c+2a·b+2b·c
=a2+b2+c2+2a·c+2a·b+2b·c
=1+1+1+2cos60°+2cos60°+2cos60°=6,
∴![]() .
.
(2)連結AC、BD,由四邊形ABCD是菱形,知BD⊥AC.
又![]() =b-a,
=b-a,![]() =(b-a)·c=b·c-a·c=0,
=(b-a)·c=b·c-a·c=0,
∴BD⊥CC1.∴BD⊥平面ACC1.
∴平面ABCD⊥平面ACC1.
故AC是AC1在平面ABCD內的射影,
∠C1AC即為AC1與平面ABCD所成的角.
∵![]() =a+b+c,
=a+b+c,![]() =a+b,
=a+b,
∴cos∠C1AC=cos〈![]() ,
,![]() 〉=
〉=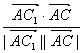 =
=![]()
故AC1與平面ABCD所成的角為arccos![]() .
.


科目:高中數學 來源: 題型:
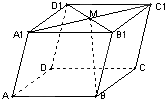 如圖:在平行六面體ABCD-A1B1C1D1中,M為A1C1與B1D1的交點.若
如圖:在平行六面體ABCD-A1B1C1D1中,M為A1C1與B1D1的交點.若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| BM |
A、-
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在平行六面體ABCD-A1B1C1D1中,已知
如圖,在平行六面體ABCD-A1B1C1D1中,已知| AB |
| AD |
| AA1 |
| a |
| b |
| c |
| BD1 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
查看答案和解析>>
科目:高中數學 來源: 題型:
 對于向量a,b,定義a×b為向量a,b的向量積,其運算結果為一個向量,且規定a×b的模|a×b|=|a||b|sinθ(其中θ為向量a與b的夾角),a×b的方向與向量a,b的方向都垂直,且使得a,b,a×b依次構成右手系.如圖,在平行六面體ABCD-EFGH中,∠EAB=∠EAD=∠BAD=60°,AB=AD=AE=2,則(
對于向量a,b,定義a×b為向量a,b的向量積,其運算結果為一個向量,且規定a×b的模|a×b|=|a||b|sinθ(其中θ為向量a與b的夾角),a×b的方向與向量a,b的方向都垂直,且使得a,b,a×b依次構成右手系.如圖,在平行六面體ABCD-EFGH中,∠EAB=∠EAD=∠BAD=60°,AB=AD=AE=2,則(| AB |
| AD |
| AE |
| A、4 | ||
| B、8 | ||
C、2
| ||
D、4
|
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在平行六面體ABCD-A1B1C1D1中,若
如圖,在平行六面體ABCD-A1B1C1D1中,若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| D1B |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2001•上海)如圖,在平行六面體ABCD-A1B1C1D1中,M為AC與BD的交點,若
(2001•上海)如圖,在平行六面體ABCD-A1B1C1D1中,M為AC與BD的交點,若| A1B1 |
| a |
| A1D1 |
| b |
| A1A |
| c |
| B1M |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com