
【題目】已知函數(shù)f(x)= ![]() ,則關(guān)于函數(shù)F(x)=f(f(x))的零點個數(shù),正確的結(jié)論是 . (寫出你認為正確的所有結(jié)論的序號)
,則關(guān)于函數(shù)F(x)=f(f(x))的零點個數(shù),正確的結(jié)論是 . (寫出你認為正確的所有結(jié)論的序號)
①k=0時,F(xiàn)(x)恰有一個零點.②k<0時,F(xiàn)(x)恰有2個零點.
③k>0時,F(xiàn)(x)恰有3個零點.④k>0時,F(xiàn)(x)恰有4個零點.
【答案】②④
【解析】解:
①當k=0時,f(x)= ![]() ,當x≤0時,f(x)=1,則f(f(x))=f(1)=
,當x≤0時,f(x)=1,則f(f(x))=f(1)= ![]() =0,
=0,
此時有無窮多個零點,故①錯誤;
②當k<0時,(Ⅰ)當x≤0時,f(x)=kx+1≥1,
此時f(f(x))=f(kx+1)= ![]() ,令f(f(x))=0,可得:x=0;
,令f(f(x))=0,可得:x=0;
(Ⅱ)當0<x≤1時, ![]() ,此時
,此時
f(f(x))=f( ![]() )=
)= ![]() ,令f(f(x))=0,可得:x=
,令f(f(x))=0,可得:x= ![]() ,滿足;
,滿足;
(Ⅲ)當x>1時, ![]() ,此時f(f(x))=f(
,此時f(f(x))=f( ![]() )=k
)=k ![]() +1>0,此時無零點.
+1>0,此時無零點.
綜上可得,當k<0時,函數(shù)有兩零點,故②正確;
③當k>0時,(Ⅰ)當x≤ ![]() 時,kx+1≤0,此時f(f(x))=f(kx+1)=k(kx+1)+1,
時,kx+1≤0,此時f(f(x))=f(kx+1)=k(kx+1)+1,
令f(f(x))=0,可得: ![]() ,滿足;
,滿足;
(Ⅱ)當 ![]() 時,kx+1>0,此時f(f(x))=f(kx+1)=
時,kx+1>0,此時f(f(x))=f(kx+1)= ![]() ,令f(f(x))=0,可得:x=0,滿足;
,令f(f(x))=0,可得:x=0,滿足;
(Ⅲ)當0<x≤1時, ![]() ,此時f(f(x))=f(
,此時f(f(x))=f( ![]() )=
)= ![]() ,令f(f(x))=0,可得:x=
,令f(f(x))=0,可得:x= ![]() ,滿足;
,滿足;
(Ⅳ)當x>1時, ![]() ,此時f(f(x))=f(
,此時f(f(x))=f( ![]() )=k
)=k ![]() +1,令f(f(x))=0得:x=
+1,令f(f(x))=0得:x= ![]() >1,滿足;
>1,滿足;
綜上可得:當k>0時,函數(shù)有4個零點.故③錯誤,④正確.
所以答案是:②④.


 開心蛙狀元作業(yè)系列答案
開心蛙狀元作業(yè)系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學業(yè)水平測試系列答案
浙江之星學業(yè)水平測試系列答案科目:高中數(shù)學 來源: 題型:
【題目】甲、乙兩人進行射擊比賽,各射擊4局,每局射擊10次,射擊命中目標得1分,未命中目標得0分.兩人4局的得分情況如下:

(1)已知在乙的4局比賽中隨機選取1局時,此局得分小于6分的概率不為零,且在4局比賽中,乙的平均得分高于甲的平均得分,求![]() 的值;
的值;
(2)如果 ![]() ,從甲、乙兩人的4局比賽中隨機各選取1局,并將其得分分別記為
,從甲、乙兩人的4局比賽中隨機各選取1局,并將其得分分別記為![]() ,求
,求![]() 的概率;
的概率;
(3)在4局比賽中,若甲、乙兩人的平均得分相同,且乙的發(fā)揮更穩(wěn)定,寫出![]() 的所有可能取值.(結(jié)論不要求證明)
的所有可能取值.(結(jié)論不要求證明)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)的定義域為(﹣2,1),則函數(shù)f(2x﹣1)的定義域為( )
A.(﹣ ![]() ,1)
,1)
B.(﹣5,1)
C.( ![]() ,1)
,1)
D.(﹣2,1)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設直線l:y=k(x+1)(k≠0)與橢圓3x2+y2=a2(a>0)相交于A、B兩個不同的點,與x軸相交于點C,記O為坐標原點. (Ⅰ)證明:a2> ![]() ;
;
(Ⅱ)若 ![]() ,求△OAB的面積取得最大值時的橢圓方程.
,求△OAB的面積取得最大值時的橢圓方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù),
為參數(shù), ![]() 為傾斜角),以坐標原點為極點,
為傾斜角),以坐標原點為極點, ![]() 軸正半軸為極軸建立極坐標系,兩種坐標系中取相同的長度單位,曲線
軸正半軸為極軸建立極坐標系,兩種坐標系中取相同的長度單位,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線![]() 的普通方程和參數(shù)方程;
的普通方程和參數(shù)方程;
(Ⅱ)設![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,求線段
兩點,求線段![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)函數(shù)![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 兩點,
兩點, ![]() ,點
,點![]() 在函數(shù)
在函數(shù)![]() 的圖象上,且
的圖象上,且![]() 為等腰直角三角形,記
為等腰直角三角形,記 ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某種商品原來每件售價為25元,年銷售量8萬件.
(Ⅰ)據(jù)市場調(diào)查,若價格每提高1元,銷售量將相應減少2000件,要使銷售的總收人不低于原收入,該商品每件定價最多為多少元?
(Ⅱ)為了擴大該商品的影響力,提高年銷售量.公司決定明年對該商品進行全面技術(shù)革新和營銷策略改革,并提高定價到x元.公司擬投入 ![]() (x2﹣600)萬元作為技改費用,投入50萬元作為固定宣傳費用,投入
(x2﹣600)萬元作為技改費用,投入50萬元作為固定宣傳費用,投入 ![]() x萬元作為浮動宣傳費用.試問:當該商品明年的銷售量a至少應達到多少萬件時,才可能使明年的銷售收入不低于原收入與總投入之和?并求出此時商品的每件定價.
x萬元作為浮動宣傳費用.試問:當該商品明年的銷售量a至少應達到多少萬件時,才可能使明年的銷售收入不低于原收入與總投入之和?并求出此時商品的每件定價.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知等比數(shù)列{an}中,a2=2,a5=128.
(1)求通項an;
(2)若bn=log2an , 數(shù)列{bn}的前n項和為Sn , 且Sn=360,求n的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
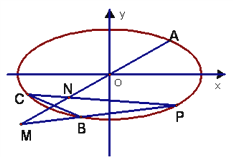
【題目】如圖,在平面直角坐標系中,已知A、B、C是橢圓![]() 上不同的三點,
上不同的三點,  ,C在第三象限,線段BC的中點在直線OA上。
,C在第三象限,線段BC的中點在直線OA上。
(1)求橢圓的標準方程;
(2)求點C的坐標;
(3)設動點P在橢圓上(異于點A、B、C)且直線PB, PC分別交直線OA于M、N兩點,證明![]() 為定值并求出該定值.
為定值并求出該定值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com