
��ƽ��ֱ������(bi��o)ϵ�У���ֱ֪��(xi��n)�ą���(sh��)�����ǣ��酢��(sh��)�����Ԟ�O�c(di��n)���S�����S��O�S�ĘO����(bi��o)ϵ�У��A�ĘO����(bi��o)���̞飮
��1����(xi��)��ֱ��(xi��n)����ͨ�����c�A��ֱ������(bi��o)���̣�
��2����ֱ��(xi��n)�ϵ��c(di��n)��A���о�(xi��n)�����о�(xi��n)�L(zh��ng)����Сֵ.
(1) ,����(xi��n)C:��2��
,����(xi��n)C:��2�� ��
��
����ԇ�}�������Ȍ��A�ĘO����(bi��o)���̻���ֱ������(bi��o)���̣��ٰ�ֱ��(xi��n)�ϵ��c(di��n)������(bi��o)��������(sh��)�����룬
������(sh��)����ֵ��(w��n)�}��Ҳ�Ɍ�ֱ��(xi��n)�ą���(sh��)���̻�����ͨ���̣�
����(j��)���ɶ����D(zhu��n)������A�ĵ�ֱ��(xi��n)����Сֵ�Ć�(w��n)�}.
ԇ�}��������1�� ,����(xi��n)C: 4��
,����(xi��n)C: 4��
��2����?y��n)�A�ĘO����(bi��o)���̞飬���ԣ�
���ԈA��ֱ������(bi��o)���̞飬�A�Ğ�,�돽��1, 6��
��?y��n)�ֱ��(xi��n)�ą���(sh��)���̞飨�酢��(sh��)����
����ֱ��(xi��n) �ϵ��c(di��n)��AC���о�(xi��n)�L(zh��ng)��
�ϵ��c(di��n)��AC���о�(xi��n)�L(zh��ng)��
��
����ֱ��(xi��n) �ϵ��c(di��n)��AC�����о�(xi��n)�L(zh��ng)����Сֵ��
�ϵ��c(di��n)��AC�����о�(xi��n)�L(zh��ng)����Сֵ�� �� 10��
�� 10��
���c(di��n)������(sh��)�����c�O����(bi��o)��ֱ��(xi��n)�c�A��λ���P(gu��n)ϵ.


 ��Уͨ���C��Ч���I(y��)ϵ�д�
��Уͨ���C��Ч���I(y��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�A�ĘO����(bi��o)���̞��2��4 �ѡ�cos
�ѡ�cos ��6��0.
��6��0.
(1)���O����(bi��o)���̻�����ͨ���̣����x��ǡ��(d��ng)?sh��)ą��?sh��)��(xi��)�����ą���(sh��)���̣�
(2)���c(di��n)P(x��y)��ԓ�A�ϣ���x��y�����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�ژO����(bi��o)ϵ�У���֪�A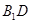 �ĈA�Ğ�
�ĈA�Ğ� ���돽��
���돽�� ���c(di��n)
���c(di��n)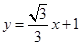 ��A
��A �Ϯ��ژO�c(di��n)
�Ϯ��ژO�c(di��n) �Ą�(d��ng)�c(di��n)������
�Ą�(d��ng)�c(di��n)������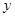 ���c(di��n)��܉�E�ĘO����(bi��o)���̣�
���c(di��n)��܉�E�ĘO����(bi��o)���̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ֱ������(bi��o)ϵxOy�У�ֱ��(xi��n)l�ą���(sh��)���̞� ��t�酢��(sh��)��0�ܦ�<�У�����ԭ�c(di��n)��O�c(di��n)��x�S�������S��O�S�����O����(bi��o)ϵ����֪����(xi��n)C�ĘO����(bi��o)���̞�
��t�酢��(sh��)��0�ܦ�<�У�����ԭ�c(di��n)��O�c(di��n)��x�S�������S��O�S�����O����(bi��o)ϵ����֪����(xi��n)C�ĘO����(bi��o)���̞�
��cos2��=4sin�ȡ�
��1����ֱ��(xi��n)l�c����(xi��n)C��ƽ��ֱ������(bi��o)���̣�
��2���O(sh��)ֱ��(xi��n)l�c����(xi��n)C���ڲ�ͬ�ă��c(di��n)A��B���� �������ֵ��
�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�O����(bi��o)ϵ�ĘO�c(di��n)�cֱ������(bi��o)ϵ��ԭ�c(di��n)�غϣ��O�S�cֱ������(bi��o)ϵ�� �S�������S�غϣ��҃�����(bi��o)ϵ����ͬ���L(zh��ng)�Ȇ�λ���AC�ą���(sh��)���̞�
�S�������S�غϣ��҃�����(bi��o)ϵ����ͬ���L(zh��ng)�Ȇ�λ���AC�ą���(sh��)���̞� ��
�� �酢��(sh��)�����c(di��n)Q�ĘO����(bi��o)��
�酢��(sh��)�����c(di��n)Q�ĘO����(bi��o)�� ��
��
��1�����AC�ą���(sh��)���̞�O����(bi��o)���̣�
��2��ֱ��(xi��n) �^(gu��)�c(di��n)Q���c�AC����M��N���c(di��n)����(d��ng)��MN���L(zh��ng)�Ȟ���С�r(sh��)��ֱ��(xi��n)
�^(gu��)�c(di��n)Q���c�AC����M��N���c(di��n)����(d��ng)��MN���L(zh��ng)�Ȟ���С�r(sh��)��ֱ��(xi��n) ��ֱ������(bi��o)���̡�
��ֱ������(bi��o)���̡�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�ژO����(bi��o)ϵ��, O��O�c(di��n), �돽��2�ĈAC�ĈA�ĵĘO����(bi��o)�� ��
��
��1����AC�ĘO����(bi��o)���̣�
��2�����ԘO�c(di��n)O��ԭ�c(di��n)���ԘO�S��x�S�����S������ֱ������(bi��o)ϵ�У�ֱ��(xi��n) �ą���(sh��)���̞�
�ą���(sh��)���̞� ��t�酢��(sh��)����ֱ��(xi��n)
��t�酢��(sh��)����ֱ��(xi��n) �c�AC�ཻ��A(y��ng)��B���c(di��n)����֪���c(di��n)
�c�AC�ཻ��A(y��ng)��B���c(di��n)����֪���c(di��n) ,��|MA|��|MB|��
,��|MA|��|MB|��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ƽ��ֱ������(bi��o)ϵxoy�У�����(xi��n)C1�ą���(sh��)���̞�  (
( ��
�� �酢��(sh��)��������O(sh��)��O�c(di��n)��x�S�������S��O�S�ĘO����(bi��o)ϵ�У�����(xi��n)C2�LjA���ژO�S�ϣ��ҽ�(j��ng)�^(gu��)�O�c(di��n)�ĈA����֪����(xi��n)C1�ϵ��c(di��n)M(1��
�酢��(sh��)��������O(sh��)��O�c(di��n)��x�S�������S��O�S�ĘO����(bi��o)ϵ�У�����(xi��n)C2�LjA���ژO�S�ϣ��ҽ�(j��ng)�^(gu��)�O�c(di��n)�ĈA����֪����(xi��n)C1�ϵ��c(di��n)M(1�� )��(du��)��(y��ng)�ą���(sh��)j��
)��(du��)��(y��ng)�ą���(sh��)j�� ������(xi��n)C2�^(gu��)�c(di��n)D(1��
������(xi��n)C2�^(gu��)�c(di��n)D(1�� )��
)��
��I��������(xi��n)C1��C2��ֱ������(bi��o)���̣�
��II�����c(di��n)A(r1��q)��B(r2��q�� )������(xi��n)C1�ϣ���
)������(xi��n)C1�ϣ��� ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�ژO����(bi��o)ϵ�У�������(xi��n)�ѣ�cos�ȣ�1�c��cos�ȣ�1�Ĺ����c(di��n)���O�c(di��n)�ľ��x��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�ژO����(bi��o)ϵ(��,��)(0�ܦ�<2��)��,������(xi��n)��=2sin���c��cos��=1�Ľ��c(di��n)Q�ĘO����(bi��o).
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com