
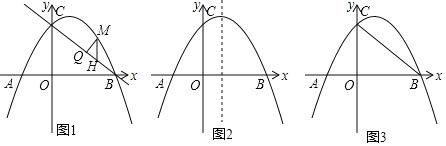
【題目】如圖1,已知拋物線y=﹣![]() x+3與x軸交于A和B兩點(diǎn),(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸交于點(diǎn)C.
x+3與x軸交于A和B兩點(diǎn),(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸交于點(diǎn)C.
(1)求出直線BC的解析式.
(2)M為線段BC上方拋物線上一動(dòng)點(diǎn),過M作x軸的垂線交BC于H,過M作MQ⊥BC于Q,求出△MHQ周長最大值并求出此時(shí)M的坐標(biāo);當(dāng)△MHQ的周長最大時(shí)在對(duì)稱軸上找一點(diǎn)R,使|AR﹣MR|最大,求出此時(shí)R的坐標(biāo).
(3)T為線段BC上一動(dòng)點(diǎn),將△OCT沿邊OT翻折得到△OC′T,是否存在點(diǎn)T使△OC′T與△OBC的重疊部分為直角三角形,若存在請(qǐng)求出BT的長,若不存在,請(qǐng)說明理由.
【答案】(1)y=﹣![]() x+3;(2)R(1,
x+3;(2)R(1,![]() );(3)BT=2或BT=
);(3)BT=2或BT=![]() .
.
【解析】
(1)由已知可求A(﹣2,0),B(4,0),C(0,3),即可求BC的解析式;
(2)由已知可得∠QMH=∠CBO,則有QH=![]() QM,MH=
QM,MH=![]() MQ,所以△MHQ周長=3QM,則求△MHQ周長的最大值,即為求QM的最大值;設(shè)M(m,
MQ,所以△MHQ周長=3QM,則求△MHQ周長的最大值,即為求QM的最大值;設(shè)M(m,![]() ),過點(diǎn)M與BC直線垂直的直線解析式為
),過點(diǎn)M與BC直線垂直的直線解析式為![]() ,交點(diǎn)
,交點(diǎn)![]() ,可求出
,可求出![]() ,當(dāng)m=2時(shí),MQ有最大值
,當(dāng)m=2時(shí),MQ有最大值![]() ;函數(shù)的對(duì)稱軸為x=1,作點(diǎn)M關(guān)于對(duì)稱軸的對(duì)稱點(diǎn)M'(0,3),連接AM'與對(duì)稱軸交于點(diǎn)R,此時(shí)|AR﹣MR|=|AR﹣M'R|=AM',|AR﹣MR|的最大值為AM';求出AM'的直線解析式為
;函數(shù)的對(duì)稱軸為x=1,作點(diǎn)M關(guān)于對(duì)稱軸的對(duì)稱點(diǎn)M'(0,3),連接AM'與對(duì)稱軸交于點(diǎn)R,此時(shí)|AR﹣MR|=|AR﹣M'R|=AM',|AR﹣MR|的最大值為AM';求出AM'的直線解析式為![]() ,則可求
,則可求![]() ;
;
(3)有兩種情況:當(dāng)TC'∥OC時(shí),GO⊥TC';當(dāng)OT⊥BC時(shí),分別求解即可.
解:(1)令y=0,即![]() ,解得
,解得![]() ,
,
∵點(diǎn)A在點(diǎn)B的左側(cè)
∴A(﹣2,0),B(4,0),
令x=0解得y=3,
∴C(0,3),
設(shè)BC所在直線的解析式為y=kx+3,
將B點(diǎn)坐標(biāo)代入解得k=![]()
∴BC的解析式為y=-![]() x+3;
x+3;
(2)∵MQ⊥BC,M作x軸,
∴∠QMH=∠CBO,
∴tan∠QMH=tan∠CBO=![]() ,
,
∴QH=![]() QM,MH=
QM,MH=![]() MQ,
MQ,
∴△MHQ周長=MQ+QH+MH=![]() QM+QM+
QM+QM+![]() MQ=3QM,
MQ=3QM,
則求△MHQ周長的最大值,即為求QM的最大值;
設(shè)M(m,![]() ),
),
過點(diǎn)M與BC直線垂直的直線解析式為![]() ,
,
直線BC與其垂線相交的交點(diǎn)![]() ,
,
∴![]() ,
,
∴當(dāng)m=2時(shí),MQ有最大值![]() ,
,
∴△MHQ周長的最大值為![]() ,此時(shí)M(2,3),
,此時(shí)M(2,3),
函數(shù)的對(duì)稱軸為x=1,
作點(diǎn)M關(guān)于對(duì)稱軸的對(duì)稱點(diǎn)M'(0,3),
連接AM'與對(duì)稱軸交于點(diǎn)R,此時(shí)|AR﹣MR|=|AR﹣M'R|=AM',
∴|AR﹣MR|的最大值為AM';
∵AM'的直線解析式為y=![]() x+3,
x+3,
∴R(1,![]() );
);
(3)①當(dāng)TC'∥OC時(shí),GO⊥TC',
∵△OCT≌△OTC',
∴![]() ,
,
∴![]()
∴BT=2;
②當(dāng)OT⊥BC時(shí),過點(diǎn)T作TH⊥x軸,
OT=![]() ,
,
∵∠BOT=∠BCO,
∴ ,
,
∴OH=![]() ,
,
∴![]()
∴BT=![]() ;
;
綜上所述:BT=2或BT=![]() .
.





| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=4,BC=6,點(diǎn)M是BC的中點(diǎn).
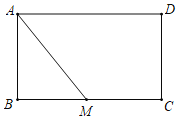
(1)在AM上求作一點(diǎn)E,使△ADE∽△MAB(尺規(guī)作圖,不寫作法);
(2)在(1)的條件下,求AE的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
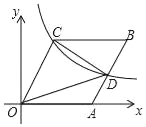
【題目】如圖,菱形OABC的一OA在x軸的正半軸上,O是坐標(biāo)原點(diǎn),tan∠AOC=![]() ,反比例函數(shù)y=
,反比例函數(shù)y=![]() 的圖象經(jīng)過點(diǎn)C,與AB交于點(diǎn)D,則△COD的面積為_____.
的圖象經(jīng)過點(diǎn)C,與AB交于點(diǎn)D,則△COD的面積為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB是⊙O的一條弦,OD⊥AB,垂足為點(diǎn)C,交⊙O于點(diǎn)D,點(diǎn)E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度數(shù);
(2)若CD=2,AB=8,求半徑的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】畢業(yè)在即,重慶實(shí)驗(yàn)外國語學(xué)校初2016級(jí)拍攝了畢業(yè)照,每個(gè)班都得到了若干張風(fēng)格迥異的照片樣品供同學(xué)們選擇.年級(jí)團(tuán)委書記王老師想了解同學(xué)們對(duì)照片的選擇情況,在全年級(jí)進(jìn)行了一次抽樣調(diào)查,按照同學(xué)們選擇的張數(shù)把選擇情況分為四個(gè)層次: A:4張;B:3張;C:2張;D:1張.并將調(diào)查結(jié)果繪制成以下條形統(tǒng)計(jì)圖和扇形統(tǒng)計(jì)圖,請(qǐng)你結(jié)合圖中信息解答下列問題:
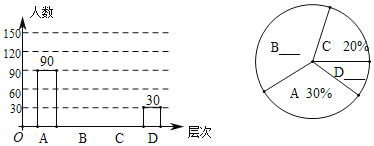
請(qǐng)你根據(jù)圖中提供的信息解答下列問題:
(1)補(bǔ)全條形統(tǒng)計(jì)圖和扇形統(tǒng)計(jì)圖;
(2)根據(jù)調(diào)查結(jié)果,估計(jì)初2016級(jí)2000名同學(xué)一共選擇了多少張畢業(yè)照?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
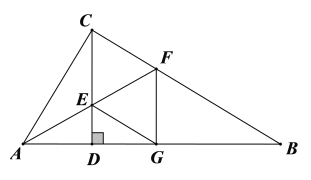
【題目】如圖,在![]() 中,
中,![]() , 垂足為
, 垂足為![]() 平分
平分![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() .
.
(1)若![]() ,求
,求![]() 的長;
的長;
(2)過點(diǎn)![]() 作
作![]() 的垂線,垂足為
的垂線,垂足為![]() ,連接
,連接![]() ,試判斷四邊形
,試判斷四邊形![]() 的形狀,并說明原因.
的形狀,并說明原因.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
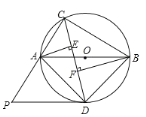
【題目】如圖,![]() 內(nèi)接于
內(nèi)接于![]() ,且
,且![]() 為
為![]() 的直徑.
的直徑.![]() 的平分線交
的平分線交![]() 于點(diǎn)
于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 的切線
的切線![]() 交
交![]() 的延長線于點(diǎn)
的延長線于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() .
.
(1)求證:![]() ;
;
(2)試猜想線段![]() ,
,![]() ,
,![]() 之間有何數(shù)量關(guān)系,并加以證明;
之間有何數(shù)量關(guān)系,并加以證明;
(3)若![]() ,
,![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com