
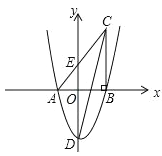
【題目】如圖,在平面直角坐標系中,△ABC 的一邊 AB 在 x 軸上,∠ABC=90°,點 C(4,8) 在第一象限內(nèi),AC 與 y 軸交于點 E,拋物線 y=![]() +bx+c 經(jīng)過 A、B 兩點,與 y 軸交于點 D(0,﹣6).
+bx+c 經(jīng)過 A、B 兩點,與 y 軸交于點 D(0,﹣6).
(1)請直接寫出拋物線的表達式;
(2)求 ED 的長;
(3)若點 M 是 x 軸上一點(不與點 A 重合),拋物線上是否存在點 N,使∠CAN=∠MAN.若存在,請直接寫出點 N 的坐標;若不存在,請說明理由.
【答案】(1)y=![]() x﹣6;(2)
x﹣6;(2)![]() ;(3) S=﹣
;(3) S=﹣![]() m2+
m2+![]() m+26(﹣2<m<4);(4)滿足條件的N點坐標為(
m+26(﹣2<m<4);(4)滿足條件的N點坐標為(![]() ,
,![]() );(
);(![]() ,﹣
,﹣![]() ).
).
【解析】(1)先確定B(4,0),再利用待定系數(shù)法求出拋物線解析式為y=![]() x2-
x2-![]() x-6;
x-6;
(2)先利用待定系數(shù)法求得直線AC的解析式為y=![]() x+
x+![]() ,則可確定E(0,
,則可確定E(0,![]() ),然后計算DE的長;
),然后計算DE的長;
(3)如圖2,當點M在x的正半軸,AN交BC于F,作FH⊥AC于H,根據(jù)角平分線的性質得FH=FB,易得AH=AB=6,再利用∠ACB的余弦可求出CF=5,則F(4,3),接著求出直線AF的解析式為y=![]() x+1,于是通過解方程組
x+1,于是通過解方程組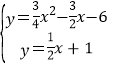 ,得N點坐標為(
,得N點坐標為(![]() ,
,![]() );當點M′在x的負半軸上時,AN′交y軸與G,先在證明∴Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下來利用待定系數(shù)法求出直線AG的解析式為y=-2x-4,然后解方程組
);當點M′在x的負半軸上時,AN′交y軸與G,先在證明∴Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下來利用待定系數(shù)法求出直線AG的解析式為y=-2x-4,然后解方程組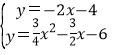 得N′的坐標.
得N′的坐標.
(1)∵BC⊥x軸,點C(4,8),
∴B(4,0),
把B(4,0),C(0,﹣6)代入y=![]() +bx+c得
+bx+c得![]() ,解得
,解得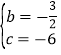 ,
,
∴拋物線解析式為y=![]() x﹣6;
x﹣6;
(2)設直線AC的解析式為y=px+q,
把A(﹣2,0),C(4,8)代入得![]() ,解得
,解得![]() ,
,
∴直線AC的解析式為y=![]() x+
x+![]() ,
,
當x=0時,y=![]() x+
x+![]() =
=![]() ,則E(0,
,則E(0,![]() ),
),
∴DE=![]() +6=
+6=![]() ;
;
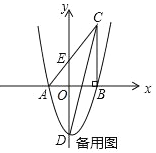
(3)如圖2,當點M在x的正半軸,AN交BC于F,作FH⊥AC于H,
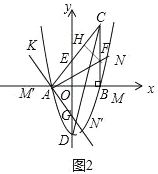
則FH=FB,
易得AH=AB=6,
∵AC=![]() ,
,
∴CH=10﹣6=4,
∵cos∠ACB=![]() ,
,
∴CF=![]() ,
,
∴F(4,3),
易得直線AF的解析式為y=![]() x+1,
x+1,
解方程組 得
得![]() 或
或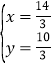 ,
,
∴N點坐標為(![]() ,
,![]() );
);
當點M′在x的負半軸上時,AN′交y軸與G,
∵∠CAN′=∠M′AN′,
∴∠KAM′=∠CAK,
而∠CAN=∠MAN,
∴∠KAC+∠CAN=90°,
而∠MAN+∠AFB=90°,
∴∠KAC=∠AFB,
而∠KAM′=∠GAO,
∴∠GAO=∠AFB,
∴Rt△OAG∽Rt△BFA,
∴![]() ,即
,即![]() ,解得OG=4,
,解得OG=4,
∴G(0,﹣4),
易得直線AG的解析式為y=﹣2x﹣4,
解方程組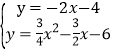 得
得![]() 或
或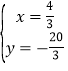 ,
,
∴N′的坐標為(![]() ,﹣
,﹣![]() ),
),
綜上所述,滿足條件的N點坐標為(![]() ,
,![]() );(
);(![]() ,﹣
,﹣![]() ).
).


科目:初中數(shù)學 來源: 題型:
【題目】本學期開學初,學校體育組對九年級某班50名學生進行了跳繩項目的測試,根據(jù)測試成績制作了下面兩個統(tǒng)計圖.
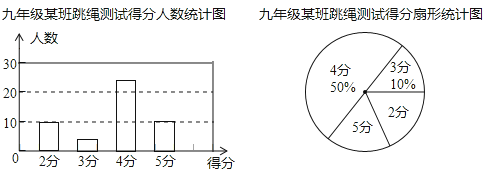
根據(jù)統(tǒng)計圖解答下列問題:
(1)本次測試的學生中,得4分的學生有多少人?
(2)本次測試的平均分是多少分?
(3)通過一段時間的訓練,體育組對該班學生的跳繩項目進行了第二次測試,測得成績的最低分為3分.且得4分和5分的人數(shù)共有45人,平均分比第一次提高了0.8分,問第二次測試中得4分、5分的學生各有多少人?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
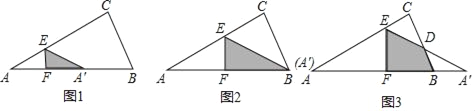
【題目】已知:如圖1,△ABC中,AB=6,AC=![]() ,BC=3,過邊AC上的動點E(點E不與點A、C重合)作EF⊥AB于點F,將△AEF沿EF所在的直線折疊得到△A'EF,設CE=x,折疊后的△A'EF與四邊形BCEF重疊部分的面積記為S.
,BC=3,過邊AC上的動點E(點E不與點A、C重合)作EF⊥AB于點F,將△AEF沿EF所在的直線折疊得到△A'EF,設CE=x,折疊后的△A'EF與四邊形BCEF重疊部分的面積記為S.
(1)如圖2,當點A'與頂點B重合時,求AE的長;
(2)如圖3,當點A'落在△ABC的外部時,A'E與BC相交于點D,求證:△A'BD是等腰三角形;
(3)試用含x的式子表示S,并求S的最大值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某市為了鼓勵居民節(jié)約用水,采用分階段計費的方法按月計算每戶家庭的水費:月用水量不超過![]() 時,按
時,按![]() 計算,月用水量超過
計算,月用水量超過![]() 時,其中的
時,其中的![]() 仍按
仍按![]() 元/
元/![]() 計算,超過部分按
計算,超過部分按![]() 元/
元/![]() 計算.設某戶家庭月用水量
計算.設某戶家庭月用水量![]() .
.
(1)用含![]() 的式子表示:
的式子表示:
當![]() 時,水費為 元;當
時,水費為 元;當![]() 時,水費為 元;
時,水費為 元;
(2)
月份 | 4月 | 5月 | 6月 |
用水量 |
|
|
|
小花家第二季度用水情況如上表,小花家這個季度共繳納水費![]() 元,請你求出小花家
元,請你求出小花家![]() 月份用水量
月份用水量![]() 的值?
的值?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
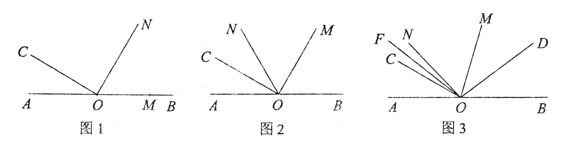
【題目】如圖1, 點![]() 在直線
在直線![]() 上,
上,![]() ,將.
,將.![]() 繞著點
繞著點![]() 以
以![]() 的速度逆時針旋轉,設旋轉時間為
的速度逆時針旋轉,設旋轉時間為![]() .
.
(1)如圖2,當![]() 平分
平分![]() 時,
時,![]() ______
______![]() ; 圖中
; 圖中![]() 的補角有: ______;
的補角有: ______;
(2)如圖3,當![]() 時,
時,![]() 平分
平分![]() ,
, ![]() 平分
平分![]() ,求
,求![]() 的度數(shù);
的度數(shù);
(3)在![]() 繞著點
繞著點![]() 逆時針旋轉的過程中,當
逆時針旋轉的過程中,當![]() ______
______![]() 時,
時,![]() .
.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
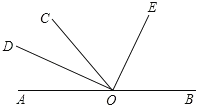
【題目】如圖,O為直線AB上一點,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)寫出圖中小于平角的角.
(2)求出∠BOD的度數(shù).
(3)小明發(fā)現(xiàn)OE平分∠BOC,請你通過計算說明道理.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】農(nóng)科所向農(nóng)民推薦渝江Ⅰ號和渝江Ⅱ號兩種新型良種稻谷.在田間管理和土質相同的條件下,Ⅱ號稻谷單位面積的產(chǎn)量比Ⅰ號稻谷低20%,但Ⅱ號稻谷的米質好,價格比Ⅰ號高.已知Ⅰ號稻谷國家的收購價是1.6元/千克.
(1)當Ⅱ號稻谷的國家收購價是多少時,在田間管理、土質和面積相同的兩塊田里分別種植Ⅰ號、Ⅱ號稻谷的收益相同?
(2)去年小王在土質、面積相同的兩塊田里分別種植Ⅰ號、Ⅱ號稻谷,且進行了相同的田間管理.收獲后,小王把稻谷全部賣給國家.賣給國家時,Ⅱ號稻谷的國家收購價定為2.2元/千克,Ⅰ號稻谷國家的收購價未變,這樣小王賣Ⅱ號稻谷比賣Ⅰ號稻谷多收入1040元,那么小王去年賣給國家的稻谷共有多少千克?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某校八年級兩個班,各選派10名學生參加學校舉行的“建模”大賽預賽,各參賽選手的成績?nèi)缦拢?/span>
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通過整理,得到數(shù)據(jù)分析表如下:
班級 | 最高分 | 平均分 | 中位數(shù) | 眾數(shù) | 方差 |
八(1)班 | 100 |
| 93 | 93 | 12 |
八(2)班 | 99 | 95 |
|
| 8.4 |
(1)直接寫出表中![]() 、
、![]() 、
、![]() 的值為:
的值為:![]() _____,
_____,![]() _____,
_____,![]() _____;
_____;
(2)依據(jù)數(shù)據(jù)分析表,有人說:“最高分在(1)班,(1)班的成績比(2)班好.”但也有人說(2)班的成績要好.請給出兩條支持八(2)班成績好的理由;
(3)學校從平均數(shù)、中位數(shù)、眾數(shù)、方差中選取確定了一個成績,等于或大于這個成績的學生被評定為“優(yōu)秀”等級,如果八(2)班有一半的學生能夠達到“優(yōu)秀”等級,認為這個成績應定為_____分.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
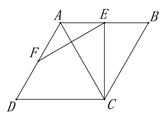
【題目】如圖,四邊形ABCD是邊長為2的菱形,E,F分別是AB,AD的中點,連接EF,EC,將△FAE繞點F旋轉180°得到△FDM.
(1)補全圖形并證明:EF⊥AC;
(2)若∠B=60°,求△EMC的面積.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com