【題目】在矩形
中，
，
，點
是邊
上一點，
交
于點
，點
在射線
上，且
是
和
的比例中項．
（1）如圖1，求證：
；
（2）如圖2，當(dāng)點在線段之間，聯(lián)結(jié)
，且與
互相垂直，求
的長；
（3）聯(lián)結(jié)，如果
與以點、、為頂點所組成的三角形相似，求
的長．
【答案】（1）詳見解析；（2）
；（3）
的長分別為
或3．
【解析】
（1）由比例中項知
，據(jù)此可證
得
，再證明
可得答案；
（2）先證
，結(jié)合
，得
，從而知
，據(jù)此可得
，由（1）得，據(jù)此知 ，求得 ；
（3）分
和
兩種情況分別求解可得．
（1）證明：∵
是
和
的比例中項
∴
∵
∴
∴
∵
∴
∵
∴
∴
∴
（2）解：∵
與
互相垂直
∴
∵
∴
∴
由（1）得
∴
∴
∴
∵
，
，
∴
∴
由（1）得
∴
∴
∴
∵
∴
∴
（3）∵
，
又
，由（1）得
∴
當(dāng)
與以點
、
、
為頂點所組成的三角形相似時
1) ，如圖
∴
由（2）得：
2），如圖
過點作
，垂足為點
由（1）得
∴
∴
又
設(shè)
，則
，
，
又
∴
，解得
∴
綜上所述，的長分別為或3．
科目：初中數(shù)學(xué) 來源： 題型：
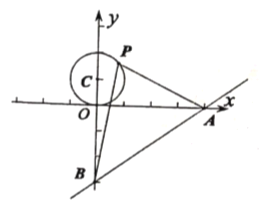
【題目】如圖，已知直線
與
軸、
軸分別交于
，
兩點，
是以
為圓心，1為半徑的圓上一動點，連接
，
，當(dāng)
的面積最大時，點的坐標(biāo)為__________．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖1，在平面直角坐標(biāo)系
中，函數(shù)
（
為常數(shù)，
，
）的圖象經(jīng)過點
和
，直線
與
軸，
軸分別交于
，
兩點.
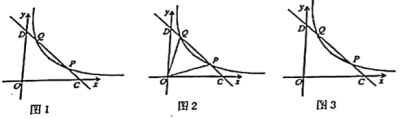
（1）求
的度數(shù)；
（2）如圖2，連接
、
，當(dāng)
時，求此時的值：
（3）如圖3，點
，點
分別在軸和軸正半軸上的動點.再以
、
為鄰邊作矩形
.若點
恰好在函數(shù)（為常數(shù)，，）的圖象上，且四邊形
為平行四邊形，求此時、的長度.
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】操場上有三根測桿AB，MN和XY，MN＝XY，其中測桿AB在太陽光下某一時刻的影子為BC(如圖中粗線)．
(1)畫出測桿MN在同一時刻的影子NP(用粗線表示)，并簡述畫法；
(2)若在同一時刻測桿XY的影子的頂端恰好落在點B處，畫出測桿XY所在的位置(用實線表示)，并簡述畫法．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如果點D、E分別在△ABC中的邊AB和AC上，那么不能判定DE∥BC的比例式是（ ）
A. AD：DB＝AE：EC B. DE：BC＝AD：AB
C. BD：AB＝CE：AC D. AB：AC＝AD：AE
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，AC是⊙O的直徑，PA切⊙O于點A，PB切⊙O于點B，且∠APB＝60°．
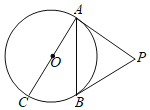
（1）求∠BAC的度數(shù)；
（2）若PA＝
，求點O到弦AB的距離．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】《九章算術(shù)》是中國傳統(tǒng)數(shù)學(xué)最重要的著作，在“勾股”章中有這樣一個問題：“今有邑方二百步，各中開門，出東門十五步有木，問：出南門幾步而見木？”
用今天的話說，大意是：如圖，
是一座邊長為200步（“步”是古代的長度單位）的正方形小城，東門
位于
的中點，南門
位于
的中點，出東門15步的
處有一樹木，求出南門多少步恰好看到位于處的樹木（即點
在直線
上）？請你計算
的長為__________步．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，以矩形ABCD的頂點A為圓心，線段AD長為半徑畫弧，交AB邊于F點；再以頂點C為圓心，線段CD長為半徑畫弧，交AB邊于點E，若AD＝
，CD＝2，則DE、DF和EF圍成的陰影部分面積是_____．
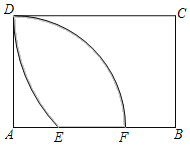
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，直線11：y1＝kx+b與反比例函數(shù)y2＝
相交于A（﹣1，4）和B（﹣4，a），直線12：y3＝﹣x+e與反比例函數(shù)y2＝相交于B、C兩點，交y軸于點D，連接OB，OC，OA．
（1）求反比例函數(shù)的解析式和c的值；
（2）求△BOC的面積；
（3）直接寫出當(dāng)kx+b≥時x的取值范圍．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com