
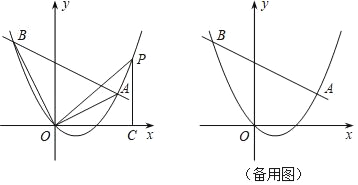
【題目】如圖,在平面直角坐標系中,直線y=kx﹣4k+4與拋物線y=![]() x2﹣x交于A、B兩點.
x2﹣x交于A、B兩點.
(1)直線總經過定點,請直接寫出該定點的坐標;
(2)點P在拋物線上,當k=﹣![]() 時,解決下列問題:
時,解決下列問題:
①在直線AB下方的拋物線上求點P,使得△PAB的面積等于20;
②連接OA,OB,OP,作PC⊥x軸于點C,若△POC和△ABO相似,請直接寫出點P的坐標.
【答案】(1)![]() ;(2)①P點坐標為
;(2)①P點坐標為![]() ,
,![]() ;②
;② ![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)直線方程化為y=k(x-4)+4,對于任意k點總有一個坐標能滿足;(2)作PQ∥y軸,求出PQ,再由S△PAB等于20,根據三角形面積計算公式即可求出相應的坐標;AO=![]() ,BO=
,BO=![]() ,AB=
,AB=![]() ,再根據勾股定理和相似三角形的定義即可求出
,再根據勾股定理和相似三角形的定義即可求出![]() ,進而可求得P3和P4的值.
,進而可求得P3和P4的值.
⑴ ![]() ;
;
直線方程化為![]() ,顯然,對于任意的k,點
,顯然,對于任意的k,點![]() 的坐標總能滿足直線方程.
的坐標總能滿足直線方程.
⑵ 當![]() 時,直線方程為
時,直線方程為![]() .
.
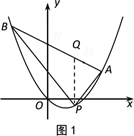
聯立方程組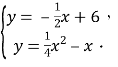 解得
解得![]() ,
,![]() .
.
① 如圖1,作![]() ∥
∥![]() 軸,交AB于點Q,則
軸,交AB于點Q,則
![]() .
.
![]()
![]() 。
。
令![]() ,即
,即![]() ,解得當
,解得當![]() 或4,相應的P點坐標為
或4,相應的P點坐標為![]() ,
,![]() ;
;
② ![]() ,
,![]() ,
,![]() ,
,![]() .
.
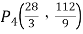
![]() ,
,![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
(i)△POC∽△ABO時,![]() .
.
即![]() .解得
.解得![]() ,
,![]() ,
,
得![]() ,
,![]() ;
;
(ii)△POC∽△BAO時,![]() .
.
即![]() .解得
.解得![]() ,
,![]() .
.
得![]() ,
,![]() .
.


科目:初中數學 來源: 題型:
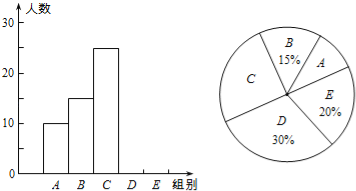
【題目】某校舉行“漢字聽寫”比賽,每位學生聽寫漢字39個,比賽結束后隨機抽查部分學生的聽寫結果,以下是根據抽查結果繪制的統計圖的一部分.
組別 | 正確字數x | 人數 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根據以上信息解決下列問題:
(1)在統計表中,m= ,n= ,并補全條形統計圖.
(2)扇形統計圖中“C組”所對應的圓心角的度數是 .
(3)若該校共有900名學生,如果聽寫正確的個數少于24個定為不合格,請你估計這所學校本次比賽聽寫不合格的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖①是數值轉換機的示意圖,圖②是小亮按照其對應關系畫出的y與x的函數圖象.已知點A的坐標為(0,3),點B的橫坐標為4.
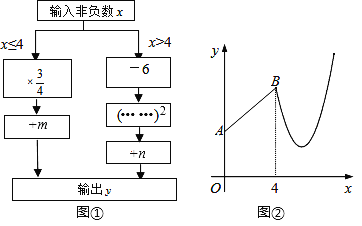
(1)求m、n的值.
(2)求輸出y的最小值.
(3)當y=4時,求x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
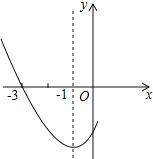
【題目】如圖,是二次函數![]() 圖象的一部分,其對稱軸是
圖象的一部分,其對稱軸是![]() ,且過點
,且過點![]() ,下列說法:
,下列說法:![]() ;
;![]() ;
;![]() ;
;![]() 若
若![]() ,
,![]() 是拋物線上兩點,則
是拋物線上兩點,則![]() ,其中正確的有
,其中正確的有![]()
![]()
A. 1個
B. 2個
C. 3個
D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程mx2﹣(m﹣1)x﹣1=0.
(1)求證:這個一元二次方程總有兩個實數根;
(2)若二次函數y=mx2﹣(m﹣1)x﹣1有最大值0,則m的值為 ;
(3)若x1、x2是原方程的兩根,且![]() =2x1x2+1,求m的值.
=2x1x2+1,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“宜居襄陽”是我們的共同愿景,空氣質量備受人們關注.我市某空氣質量監測站點檢測了該區域每天的空氣質量情況,統計了2013年1月份至4月份若干天的空氣質量情況,并繪制了如下兩幅不完整的統計圖.
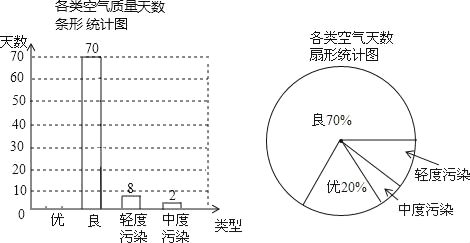
請根據圖中信息,解答下列問題:
(1)統計圖共統計了 天的空氣質量情況;
(2)請將條形統計圖補充完整;空氣質量為“優”所在扇形的圓心角度數是 ;
(3)從小源所在環保興趣小組4名同學(2名男同學,2名女同學)中,隨機選取兩名同學去該空氣質量監測站點參觀,則恰好選到一名男同學和一名女同學的概率是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
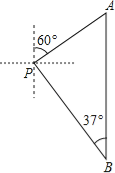
【題目】小亮一家在一湖泊中游玩,湖泊中有一孤島,媽媽在孤島P處觀看小亮與爸爸在湖中劃船(如圖所示).小船從P處出發,沿北偏東60°方向劃行200米到A處,接著向正南方向劃行一段時間到B處.在B處小亮觀測到媽媽所在的P處在北偏西37°的方向上,這時小亮與媽媽相距多少米(精確到1米)?
(參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知矩形ABCD的三個頂點B(4,0)、C(8,0)、D(8,8).拋物線y=ax2+bx過A、C兩點.
(1)直接寫出點A的坐標,并求出拋物線的解析式;
(2)動點P從點A出發.沿線段AB向終點B運動,同時點Q從點C出發,沿線段CD向終點D運動.速度均為每秒1個單位長度,運動時間為t秒.過點P作PE⊥AB交AC于點E
①過點E作EF⊥AD于點F,交拋物線于點G.當t為何值時,線段EG最長?
②連接EQ.在點P、Q運動的過程中,判斷有幾個時刻使得△CEQ是等腰三角形?請直接寫出相應的t值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com