
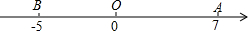
分析 (1)根據點A、B表示的數利用兩點間的距離公式即可求出線段AB的長度,再根據點P、Q運動的方向及速度即可找出點P、Q表示的數;
(2)當點P追上點Q時,結合點P、Q表示的數相等即可得出關于t的一元一次方程,解之即可得出結論;當點B恰為PQ的中點時,結合點P、B、Q表示的數之間的關系即可得出關于t的一元一次方程,解之即可得出結論;
(3)分t≤-7、-7<t≤5以及t>5三種情況去絕對值,由此即可得出結論.
解答 解:(1)線段AB的長度為7-(-5)=12,
當運動時間為t秒時,點P表示的數為7-3t,點Q表示的數為-t.
故答案為:12;7-3t;-t.
(2)當點P追上點Q時,有7-3t=-t,
解得:t=$\frac{7}{2}$;
當點B恰為PQ的中點時,有2×(-5)=7-3t+(-t),
解得:t=$\frac{17}{4}$.
(3)當t≤-7時,|t+7|-|5-t|=-t-7-5+t=-12,
∵-12≠-12,
∴t≤-7不合適;
當-7<t≤5時,|t+7|-|5-t|=t+7-5+t=2t+2=12,
解得:t=5.
當t>5時,|t+7|-|5-t|=t+7-t+5=12,
∵12=12,
∴t>5.
綜上所述:t的范圍是t≥5.
故答案為:t≥5.
點評 本題考查了一元一次方程的應用、絕對值以及整式的加減,根據數量關系找出關于t的一元一次方程是解題的關鍵.


 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:初中數學 來源: 題型:選擇題
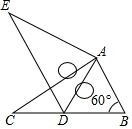 如圖,將Rt△ABC繞點A按順時針旋轉一定角度得到Rt△ADE,點B的對應點D恰好落在BC邊上.若AB=1,∠B=60°,則CD的長為( )
如圖,將Rt△ABC繞點A按順時針旋轉一定角度得到Rt△ADE,點B的對應點D恰好落在BC邊上.若AB=1,∠B=60°,則CD的長為( )| A. | 0.5 | B. | 1.5 | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com