Question

定理：圖1，如果∠ADB=∠ACB，那么四邊形ABCD有外接圓，也叫做A，B，C，D四點共圓．（注：本定理不需要證明）
（1）圖2，△ABC中，AC=BC，點E，F分別在線段AC，BC上運動（不與端點重合），而且CE=BF，O是△ABC的外心（外接圓的圓心，它到三角形三個頂點距離相等），試證明C，E，O，F四點共圓．（注：可以使用上述定理，也可以采用其他方法）

如果將問題2中的點C“分離”成兩個點，那么就有：
（2）圖3，在凸四邊形ABCD中，AD=BC，點E，F分別在線段AD，BC上運動（不與端點重合），而且DE=BF，直線AC，BD相交于點P，直線EF，BD相交于點Q，直線EF，AC相交于點R．當點E，F分別在線段AD，BC上運動（不與端點重合）時，探究△PQR的外接圓是否經過除點P外的另一個定點？如果是，請給出證明，并指出是哪個定點；如果不是，請說明理由．

Answer 1

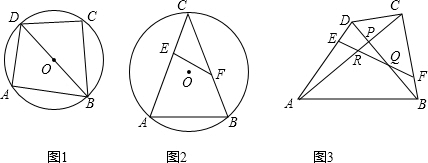
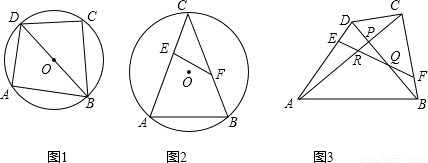
證明：（1）∵OB=0C，
∴∠OCB=∠OBC，
又∵AC=BC，
∴∠OCB=∠OCA，
∴∠OBC=∠OCA，
在△ECO與△FBO中，，
∴△ECO≌△FBO，
∴∠EOC=∠FOB，又∠AOC=∠BOC，
∴∠EOF=∠COB，
又∵EO=OF，
∴∠OEF=∠OCF，
∴C，E，O，F四點共圓；

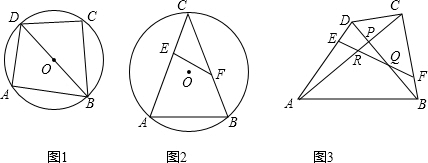
（2）由于是將問題2中的點C“分離”成兩個點，
根據圖形變換的過程，猜測△PQR的外接圓一定經過線段AC，BD垂直平分線的交點O．
下面給予證明：
顯然△ODA≌△OCB，
∴∠OBF=∠ODE，
∴△OBF≌△ODE，
∴OE=OF且∠BOF=∠DOE，
∴∠BOD=∠EOF，
∴△EOF∽△BOD∽△COA，
∴∠OBD=∠OEF=∠OCA，
∴O，B，F，Q四點共圓，O，F，C，R四點也共圓，
∴∠OFB=∠OQB=∠ORP，
∴P，Q，O，R四點共圓，即當點E和F變動時，△PQR的外接圓經過除點P外的另一個定點O．

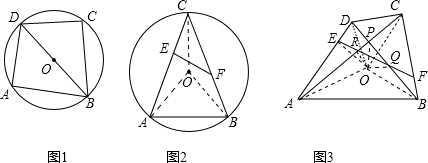
分析：（1）根據外心的性質可知OA=OB=OC，則∠OCB=∠OBC，又AC=BC，由等腰三角形的對稱性，得∠OCB=∠OCA，再根據已知條件證明△ECO≌△FBO，可得∠EOC=∠FOB，OE=OF，比較等腰△OEF與等腰△OBC的頂角，可得底角∠OFE=∠OBC=∠OCE，可證C，E，O，F四點共圓；
（2）本題要找出第四個點O，使P、Q、R、O四點共圓，作線段AC，BD垂直平分線的交點O，由垂直平分線的性質得OA=OC，OD=OB，AD=BC，可證△ODA≌△OCB，∠OBF=∠ODE，進一步證明△OBF≌△ODE，可得OE=OF且∠BOF=∠DOE，從而有∠BOD=∠EOF，得到△EOF∽△BOD∽△COA，利用相似得角的等量關系，證明四點共圓．
點評：本題考查了四點共圓，全等三角形的判定與性質，外心的性質．關鍵是構造到三角形三頂點（四邊形四頂點）距離相等的點，證明四點共圓．