
【題目】如圖,在8×6正方形方格中,點A、B、C在小正方形的頂點上.
(1)在圖中畫出與△ABC關于直線![]() 成軸對稱的△AB′C′,并回答問題:
成軸對稱的△AB′C′,并回答問題:
圖中線段CC′被直線l ;
(2)在直線l上找一點D,使線段DB+DC最短.(不寫作法,應保留作圖痕跡)
(3) 在直線l確定一點P,使得|PA-PB|的值最小.(不寫作法,應保留作圖痕跡)
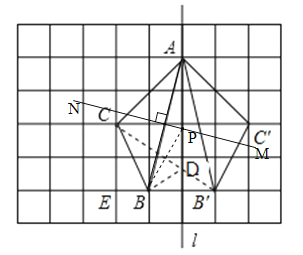
【答案】(1)詳見解析;(2)詳見解析;(3) 詳見解析.
【解析】試題分析:(1)根據網格結構找出點B、C關于直線l的對稱點B′、C′的位置,然后順次連接即可,根據軸對稱的性質,對稱軸垂直平分對稱點的連線;
(2)根據軸對稱確定最短路線,連接B′C,與對稱軸l的交點即為所求點D;
(3)作線段AB的中垂線EF交直線l于點P,則PA=PB,即|PA-PB|=0最短.
試題解析:解:(1)如圖所示,∵△ABC與△AB′C′關于直線l成軸對稱,∴線段CC′被直線l垂直平分;
(2)連接B′C,交直線l與點P,此時PB+PC的長最短;
(3)作線段AB的中垂線EF交直線l于點P,則PA=PB,即|PA-PB|=0最短.


科目:初中數學 來源: 題型:
【題目】⑴例:代數式![]() 表示
表示![]() 、
、![]() 兩數和的平方. 仿照上例填空:
兩數和的平方. 仿照上例填空:
代數式![]() 表示________________________________________.
表示________________________________________.
代數式![]() 表示________________________________________.
表示________________________________________.
⑵試計算![]() 、
、![]() 取不同數值時,
取不同數值時, ![]() 及
及![]() 的植, 填入下表:
的植, 填入下表:
| 當 | 當 | 當 |
| |||
|
⑶請你再任意給![]() 、
、![]() 各取一個數值, 并計算
各取一個數值, 并計算![]() 及
及![]() 的植:
的植:
當![]() =_____,
=_____, ![]() =______時,
=______時, ![]() =_________,
=_________, ![]() =__________.
=__________.
⑷我的發現: ______________________________.
⑸用你發現的規律計算: ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB與半徑為2的⊙O相切于點C,點D、E、F是⊙O上三個點,EF∥AB,若EF=![]() ,則∠EDC的度數為( )
,則∠EDC的度數為( )
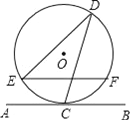
A. 60° B. 90° C. 30° D. 75°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,動點P從點A出發沿AD方向向點D以1cm/s的速度運動,動點Q從點C開始沿著CB方向向點B以3cm/s的速度運動.點P、Q分別從點A和點C同時出發,當其中一點到達端點時,另一點隨之停止運動. 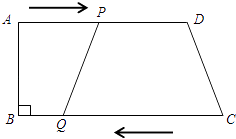
(1)經過多長時間,四邊形PQCD是平行四邊形?
(2)經過多長時間,四邊形PQBA是矩形?
(3)經過多長時間,當PQ不平行于CD時,有PQ=CD.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com