【題目】有一類隨機事件概率的計算方法：設試驗結果落在某個區域S中的每一點的機會均等，用A表示事件“試驗結果落在S中的一個小區域M中”，那么事件A發生的概率P（A）=
． 有一塊邊長為30cm的正方形ABCD飛鏢游戲板，假設飛鏢投在游戲板上的每一點的機會均等．求下列事件發生的概率：
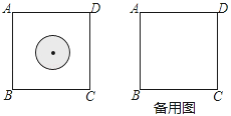
(1)在飛鏢游戲板上畫有半徑為5cm的一個圓（如圖1），求飛鏢落在圓內的概率；
(2)飛鏢在游戲板上的落點記為點O，求△OAB為鈍角三角形的概率．
【答案】（1）P（飛鏢落在圓內）
；（2）P（△OAB為鈍角三角形）
【解析】
（1）分別計算半徑為5cm的圓的面積和邊長為30cm的正方形ABCD的面積，然后計算
即可求出飛鏢落在圓內的概率；
（2）根據題意及結合圖形可得：當點O落在以AB為直徑的半圓內△OAB為鈍角三角形，然后計算以AB為直徑的半圓的面積，然后用半圓的面積除以正方形的面積即可求△OAB為鈍角三角形的概率．
（1）∵半徑為5cm的圓的面積=π52=25πcm2 ，
邊長為30cm的正方形ABCD的面積=302=900cm2 ，
∴P（飛鏢落在圓內）=半徑為5cm的圓的面積/邊長為30cm的正方形ABCD的面積=
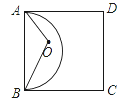
（2）如圖可得：當點O落在以AB為直徑的半圓內△OAB為鈍角三角形．
∵S半圓=
π152=
，
∴P（△OAB為鈍角三角形）=
科目：初中數學 來源： 題型：
【題目】小紅想利用陽光下的影長測量學校旗桿AB的高度．如圖，他在某一時刻在地面上豎直立一個2米長的標桿CD，測得其影長DE=0.4米．
（1）請在圖中畫出此時旗桿AB在陽光下的投影BF．
（2）如果BF=1.6，求旗桿AB的高．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將半徑為2，圓心角為120°的扇形OAB繞點A逆時針旋轉60°，點O，B的對應點分別為O′，B′，連接BB′，則圖中陰影部分的面積是( )
A. 
B. 2
－
C. 2－ D. 4－
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在等腰△ABC與等腰△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE，且點D、E、C三點在同一條直線上，連接BD．
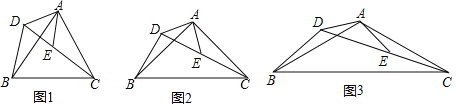
（1）如圖1，求證：△ADB≌△AEC
（2）如圖2，當∠BAC＝∠DAE＝90°時，試猜想線段AD，BD，CD之間的數量關系，并寫出證明過程；
（3）如圖3，當∠BAC＝∠DAE＝120°時，請直接寫出線段AD，BD，CD之間的數量關系式為： （不寫證明過程）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】反比例函數
的圖象的一支在第一象限，A（﹣1，a）、B（﹣3，b）均在這個函數的圖象上．
（1）圖象的另一支位于什么象限？常數n的取值范圍是什么？
（2）試比較a、b的大小；
（3）作AC⊥x軸于點C，若△AOC的面積為5，求這個反比例函數的表達式．
查看答案和解析>>
科目：初中數學 來源： 題型：
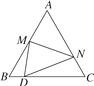
【題目】如圖，等邊△ABC的邊長為30，點M為線段AB上一動點，將等邊△ABC沿過點M的直線折疊，使點A落在直線BC上的點D處，且BD∶DC＝1∶4，折痕與直線AC交于點N，則AN的長為________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一個工人拿一個
米長的梯子，底端
放在距離墻根
點
米處，另一端點
點靠墻．
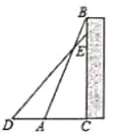
（1）求這個梯子的頂端距離地面的高度
；
（2）如圖，如果梯子的頂部下滑
米，那么梯子的底部向外滑多少米．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
