
【題目】如圖,點P是菱形ABCD的對角線AC上的一個動點,過點P垂直于AC的直線交菱形ABCD的邊于M、N兩點.設AC=2,BD=1,AP=x,△CMN的面積為y,則y關于x的函數圖象大致形狀是( )

科目:初中數學 來源: 題型:
【題目】小華是花店的一名花藝師,她每天都要為花店制作普通花束和精致花束,她每月工作20天,每天工作8小時,她的工資由基本工資和提成工資兩部分構成,每月的基本工資為l800元,另每制作一束普通花束可提2元,每制作一束精致花束可提5元.她制作兩種花束的數量與所用時間的關系見下表:
制作普通花束(束) | 制作精致花束(束) | 所用時間(分鐘) |
10 | 25 | 600 |
15 | 30 | 750 |
請根據以上信息,解答下列問題:
(1)小華每制作一束普通花束和每制作一束精致花束分別需要多少分鐘?
(2)2019年11月花店老板要求小華本月制作普通花束的總時間![]() 不少于3000分鐘且不超過5000分鐘,則小華該月收入
不少于3000分鐘且不超過5000分鐘,則小華該月收入![]() 最多是多少元?此時小華本月制作普通花束和制作精致花束分別是多少束?
最多是多少元?此時小華本月制作普通花束和制作精致花束分別是多少束?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,過正方形ABCD頂點B,C的⊙O與AD相切于點P,與AB,CD分別相交于點E,F,連接EF.
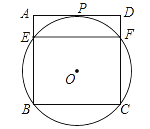
(1)求證:PF平分∠BFD;
(2)若tan∠FBC= ![]() ,DF=
,DF=![]() ,求EF的長.
,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【問題情境】
已知矩形的面積為a(a為常數,a>0),當該矩形的長為多少時,它的周長最小?最小值是多少?
【數學模型】
設該矩形的長為x,周長為y,則y與x的函數表達式為y=2(x+![]() )(x>0).
)(x>0).
【探索研究】
小彬借鑒以前研究函數的經驗,先探索函數y=x+![]() 的圖象性質.
的圖象性質.
(1)結合問題情境,函數y=x+![]() 的自變量x的取值范圍是x>0,下表是y與x的幾組對應值.
的自變量x的取值范圍是x>0,下表是y與x的幾組對應值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①寫出m的值;
②畫出該函數圖象,結合圖象,得出當x= 時,y有最小值,y最小= ;
提示:在求二次函數y=ax2+bx+c(a≠0)的最大(小)值時,除了通過觀察圖象,還可以通過配方得到.試用配方法求函數y=x+![]() (x>0)的最小值,解決問題(2)
(x>0)的最小值,解決問題(2)
【解決問題】
(2)直接寫出“問題情境”中問題的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
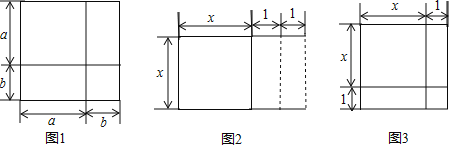
【題目】(1)請用兩種不同的方法列代數式表示圖1的面積
方法1 ,
方法2 ;
(2)若a+b=7,ab=15,根據(1)的結論求a2+b2的值;
(3)如圖2,將邊長為x和x+2的長方形,分成邊長為x的正方形和兩個寬為1的小長方形,并將這三個圖形拼成圖3,這時只需要補一個邊長為1的正方形便可以構成一個大正方形.
①若一個長方形的面積是216,且長比寬大6,求這個長方形的寬.
②把一個長為m,寬為n的長方形(m>n)按上述操作,拼成一個在一角去掉一個小正方形的大正方形,則去掉的小正方形的邊長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為迎接體育中考,了解學生的體育情況,學校隨機調查了本校九年級50名學生“30秒跳繩”的次數,并將調查所得的數據整理如下:

根據以上圖表信息,解答下列問題:
(1)表中的a= ,c= ;
(2)請把頻數分布直方圖補充完整;(畫圖后請標注相應的數據)
(3)若該校九年級共有500名學生,請你估計“30秒跳繩”的次數60次以上(含60次)的學生有多少人
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察表一,尋找規律,表二、表三、表四分別是從表一中截取的一部分,其中![]() ,
,![]() ,
,![]() 的值分別為( )
的值分別為( )
表一
|
|
|
| … |
|
|
|
| … |
|
|
|
| … |
|
|
|
| … |
… | … | … | … | … |
表二
|
|
|
表三
|
|
|
|
表四
| |
| |
|
A.![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]() C.
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝廠生產一種西裝和領帶,西裝每套定價![]() 元,領帶每條定價
元,領帶每條定價![]() 元,廠方在開展促銷活動期間,向客戶提供兩種優惠方案:
元,廠方在開展促銷活動期間,向客戶提供兩種優惠方案:
①買一套西裝送一條領帶;
②西裝和領帶都按定價的![]() 付款.
付款.
現某客戶要到該服裝廠購買西裝![]() 套,領帶
套,領帶![]() 條(
條(![]() ).
).
(1)客戶分別按方案①、方案②購買,各需付款多少元?(用含![]() 的代數式表示);
的代數式表示);
(2)若![]() ,通過計算說明此時按哪種方案購買較為合算?
,通過計算說明此時按哪種方案購買較為合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按要求作圖,不要求寫做法,但要保留作圖痕跡.
(1)如圖1,四邊形ABCD是平行四邊形,E為BC上任意一點,請只用直尺(不帶刻度)在邊AD上找點F,使DF=BE.

(2)如圖2,BE是菱形ABCD的邊AD上的高,請只用直尺(不帶刻度)作出菱形ABCD的邊AB上的高DF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com